| Die Quadratur des Kreises
als Näherungslösung |
 |
|||||||||
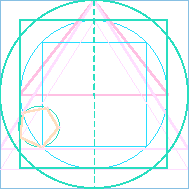
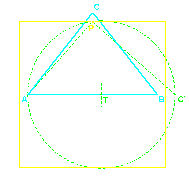
| Die Quadratur des Kreises als
Näherung, Beispiele aus Architektur, Kunst und Esoterik Historisches zur Zahl PI und gebrochen rationale Näherungswerte für PI |
||||||||||
   |
1.1 Pi im Altertum 1.2 Pi in der Moderne 2.1 Quadratur 1 2.2 Genauigkeit 1 2.3 Genauigkeit 2 3.1 Quadratur 2 3.2 Genauigkeit 1 3.3 Genauigkeit 2 4.1 Erweiterung 1 4.2 Erweiterung 2 4.3 Erweiterung 3 5.1 Quadratur 3 6.1 Quadratur und Fünfeck 1 6.2 Quadratur und Fünfeck 2 Ergänzungen 7.1 Quadratur und Proportion 7.2 Sakrale Architektur 7.3 Beispiele aus der Architektur 7.4 Quadratur und Esotetik 7.5 Quadratur und Geomantie 8.1 Quadratur und Gizeh 1 8.2 Quadratur und Gizeh 2 8.3 Quadratur und Gizeh 3 9.1 Quadratur und Ruhrgebiet 1 9.2 Quadratur und Ruhrgebiet 2 9.3 Quadratur und Ruhrgebiet 3 9.4 Quadratur und Ruhrgebiet 4 |
  letztes update: 01.02.2011 Impressum  |
||||||||
 |
||||||||||
