DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 1.3.0 | Reihenentwicklungen für π | ||
| 1.3.1 | John Wallis | 1616 - 1703 | |
| 1.3.2 | William Brouncker | 1620 - 1684 | |
| 1.3.3 | James Gregory | 1638 - 1675 | |
| 1.3.4 | Isaac Newton | 1643 - 1727 | |
| 1.3.5 | Gottfried Wilhelm Leibnitz | 1646 - 1716 | |
| 1.3.6 | Abraham Sharp | 1653 -1742 | |
| 1.3.7 | John Machin | 1680 - 1751 | |
| 1.3.8 | Georg Freiherr von Vega | 1754 - 1802 | |
| 1.3.9 | π als Symbol | ||
| 1.3.10 | Leonhard Euler | 1707 - 1783 | |
| 1.3.11 | Lambert und die Irrtionalität von π | 1728 -1777 | |
| 1.3.12 | Adrien-Marie Legendre | 1752 - 1833 | |
| 1.3.13 | Carl Frdiedrich Gauß | 1777 - 1855 | |
| 1.3.14 | Joseph Liouville | 1809 -1882 | |
| 1.3.15 | Charles Hermite und die Transzendens von π | 1822 -1901 | |
| 1.3.16 | Lindemann und π als transzendente Zahl | 1852 - 1939 | |
| 1.3.17 | David Hilbert | 1862 - 1943 | |
| 1.3.18 | Ramanujan | 1887 - 1920 | |
| 1.3.19 | Geometrische Näherungskonstruktionen | 1849 - 1961 | |
| 1.3.20 | Bailey, Borwein, Plouffe | 1961 | |
| 1.3.21 | Die Jagd nach Stellen von π | ||
| Der rein geometrische Ansatz zur
Bestimmung der Kreiskonstanten war mit Huygens Arbeit im
wesentlichen ausgeschöpft. Bessere Näherungen ergaben
sich mit Hilfe von unendlichen Reihen, speziell der
Reihenentwicklung trigonometrischer Funktionen. Zwar hatte François Viète schon Ende des 16. Jahrhunderts durch die Betrachtung bestimmter Streckenverhältnisse aufeinanderfolgender Polygone eine erste exakte Darstellung von π durch ein unendliches Produkt gefunden, doch erwies sich diese Formel als unhandlich. Eine einfachere Reihe, die darüber hinaus nur mit rationalen Operationen auskommt, stammt von John Wallis, eine weitere Darstellung der Kreiszahl als Kettenbruch von William Brouncker. Wichtiger für die Praxis war die von James Gregory und davon unabhängig von Gottfried Wilhelm Leibniz gefundene Reihe für den Arcustangens. Obwohl diese Reihe selbst nur langsam konvergiert, kann man aus ihr andere Reihen ableiten, die sich wiederum sehr gut zur Berechnung der Kreiszahl eignen. Anfang des 18. Jahrhunderts waren mit Hilfe solcher Reihen über 100 Stellen von π berechnet, neue Erkenntnisse über das Problem der Kreisquadratur konnten dadurch allerdings nicht gewonnen werden. |
| John
Wallis (23. November-jul./ 3. Dezember 1616-greg.-
28. Oktober-jul./ 8. November 1703-greg.) war ein
englischer Mathematiker, der Beiträge zur
Infinitesimalrechnung und zur Berechnung der Kreiszahl
π leistete. In seiner Algebra ließ er auch komplexe Lösungen von Gleichungen zu. Er war einer der ersten britischen Mathematiker, die die Methoden der analytischen Geometrie von Descartes benutzten. Unter anderem wandte er sie auf die Kegelschnitte an. In seiner Algebra, seinem letzten großen Werk, an dem er viele Jahre arbeitete, ist auch ein Abschnitt über unendliche Reihen und sie enthält insbesondere in der ersten Auflage die ersten Veröffentlichungen von einigen von Newtons Resultaten auf diesem Feld. Wallis war sehr bemüht Newtons Priorität auf diesem Gebiet zu dokumentieren (zumal Newton damals nichts selbst veröffentlichte) und ermunterte auch andere Kollegen in Großbritannien dazu. In seiner Algebra baute er insbesondere auf der Arbeit englischer Mathematiker wie Oughtred, Harriot und John Pell auf. Er versuchte auch nachzuweisen, dass Descartes in der Algebra von Harriot beeinflusst war. John Wallis verfasste Abhandlungen zur Musiktheorie und ein Buch über Phonetik (De loque-la, zuerst 1652), das viele Auflagen erlebte (6. Auflage 1765). Wallis Studien über Phonetik führten auch zu Methoden zur Unterrichtung tauber Kinder. Zur Bewegungslehre und Mechanik verfasste er 1671 ein Werk Mechanica sive de motu tractatus geometricus, in dem er auf galileischer Grundlage die strikt geometrische Grundla-ge dieser Lehre betonte. Es handelt insbesondere von Schwerpunkten und Stössen und stellte einen wesentlichen Fortschritt in der Mathematisierung der Mechanik im 17. Jahrhundert dar. Das Buch beeinflusste auch Isaac Newton stark, der mit seinem Buch Principia (1687) allerdings weit darüber hinausging. Wallis trug in seinen Werken zur Entwicklung der Infinitesimalrechnung vor Newton bei, wobei er auf den Arbeiten von Johannes Kepler, Cavalieri, Roberval und Torricelli aufbaute. 1656 leitete er in Arithmetica Infinitorum, in dem er Untersuchungen zu unendlichen Reihen veröffentlichte, das Wallissche Produkt her, mit dem man näherungsweise die Kreiszahl π berechnen kann: |
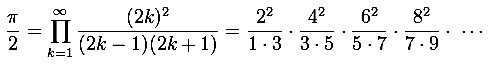
|
| William
Brouncker, 2. Viscount Brouncker FRS (1620 -
5. April 1684) war ein irischer Mathematiker und 1660
Gründungsmitglied der Royal Society in London. Brouncker erhielt seine Ausbildung in Oxford. Er ist bekannt für seine Arbeiten über Kettenbrüche und über die Berechnung von Logarithmen durch unendliche Reihen. Er produzierte auch einige Lösungen der Pellschen Gleichung a x2 + 1 = y2. 1655 fand Brouncker, aufgrund der Gleichung von Wallis, eine Kettenbruchdarstellung für den Kehrwert von π/4 : |
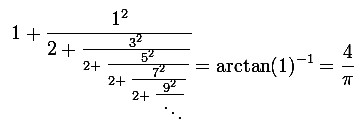 |
| James
Gregory (November 1638 - Oktober 1675) war ein
schottischer Mathematiker und Astronom. Er fand
wesentliche Resultate der Analysis vor oder gleichzeitig
mit seinen Zeitgenossen, publizierte jedoch wenig. Nach seinem Abschluss 1657 schrieb Gregory ein Buch über seine Forschungen in der Optik, die Optica Promota. Darin beschäftigt er sich mit Linsen, Reflexion, Brechung, Parallaxen und der erstmaligen Verwendung von photometrischen Methoden zur Entfernungsmessung. Er schlug auch vor, Venustransite zur Bestimmung der astronomischen Einheit zu beobachten, ein Vorschlag, der später von Edmund Halley ohne Erwähnung der Priorität Gregorys wiederholt wurde. Die bedeutendste Entwicklung ist allerdings die Beschreibung eines Spiegelteleskops, das mit einem sekundären konkaven Spiegel das reflektierte Licht des primären Parabolspiegels durch ein kleines Loch im Primärspiegel auf das Okular lenkt. Als Gregory-Teleskop bekannt, wurde diese Bauform bis in das 19. Jahrhundert verwendet. Von London aus reiste er 1664 über Paris nach Padua, wo er in Zusammenarbeit mit Stefano degli Angeli (1623–1697) an der Berechnung von Kreis- und Parabelflächen durch unendliche konvergente Reihen arbeitete. Dort entstand 1667 das Buch Vera circuli et hyperbolae quadratura, in dem er sich mit den Grundlagen der Differentialrechnung beschäftigte und Geometriae pars universalis (1668), das den ersten bekannten Beweis für den Hauptsatz der Analysis enthält. Im gleichen Werk ermittelte er den Abstand zu Sirius durch photometrischen Vergleich mit Jupiter zu 1,25 Lichtjahren statt des heutigen Werts von 8.6 LJ. Nach seiner Rückkehr nach London 1668 wurde er zum Fellow der Royal Society berufen und erhielt im selben Jahr einen Lehrstuhl für Mathematik an der Universität St Andrews. Sicher ist, dass er in diesem Sommer die Taylor-Reihen von Sinus und Kosinus sowie des Tangens kannte. Wichtig für die Praxis war die von James Gregory und davon unabhängig von Gottfried Wilhelm Leibniz gefundene Reihe für den Arcustangens. |
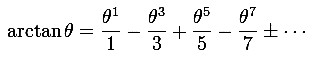
|
| Dieses erschloss neue Wege bei der Berechnung der Kreiszahl π. Die obige Reihe ist wegen arctan 1 = π/4 auch ein Spezialfall der Reihenentwicklung des Arcustangens. Sie war Grundlage vieler Approximationen von π in der folgenden Zeit. |
| Sir Isaac
Newton (25. Dezember 1642-jul./ 4. Januar
1643-greg. - 20. März 1726-jul./ 31. März 1727-greg.)
war ein englischer Naturforscher und Verwaltungsbeamter. Isaac Newton ist der Verfasser der Philosophiae Naturalis Principia Mathematica, in denen er mit seinem Gravitationsgesetz die universelle Gravitation und die Bewegungsgesetze beschrieb und damit den Grundstein für die klassische Mechanik legte. Fast gleichzeitig mit Gottfried Wilhelm Leibniz entwickelte Newton die Infinitesimalrechnung. Er verallgemeinerte das Binomische Theorem mittels unendlicher Reihen auf beliebige reelle Exponenten. Bekannt ist er auch für seine Leistungen auf dem Gebiet der Optik: die von ihm verfochtene Teilchentheorie des Lichtes und die Erklärung des Spektrums. Aufgrund seiner Leistungen, vor allem auf den Gebieten der Physik und Mathematik, gilt Sir Isaac Newton als einer der bedeutendsten Wissenschaftler aller Zeiten. Die Principia Mathematica werden als eines der wichtigsten wissenschaftlichen Werke eingestuft. Zusätzlich zu seinen fundamentalen Leistungen zur Physik war Newton neben Gottfried Wilhelm Leibniz einer der Begründer der Infinitesimalrechnung und erbrachte wichtige Beiträge zur Algebra. Zu seinen frühesten Leistungen zählt eine verallgemeinerte Formulierung des Binomischen Theorems mit Hilfe von unendlichen Reihen. Er bewies, dass es für sämtliche reellen Zahlen (also auch negative und Brüche) gültig ist. Durch die Ausarbeitung der Analysis, von Isaac Newton konnten bessere Näherungswerte von π gefunden werden. Zwei seiner Reihen zur Berechnung von π sind die folgenden: |
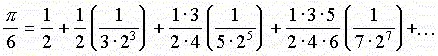
|
| Newton verfügte 1665 über 16 Stellen von π. Dies geschah durch obige Reihenentwicklungen, die dann allerdings noch in mühsamer Handarbeit umgesetzt werden mussten. |
| Gottfried
Wilhelm Leibniz (21. Juni-jul./ 1. Juli
1646-greg. -14. November 1716) war ein deutscher
Philosoph und Wissenschaftler, Mathematiker, Diplomat,
Physiker, Historiker, Politiker, Bibliothekar und Doktor
des weltlichen und des Kirchenrechts in der frühen
Aufklärung. Er gilt als der universale Geist seiner Zeit
und war einer der bedeutendsten Philosophen des
ausgehenden 17. und beginnenden 18. Jahrhunderts sowie
einer der wichtigsten Vordenker der Aufklärung. Leibniz befasste sich intensiv mit Logik und propagierte erstmals eine symbolische Logik in Kalkülform. Seine Logikkalkül-Skizzen veröffentlichte er allerdings nicht; erst sehr verspätet (1840, 1890, 1903) wurden sie publiziert. Seine charakteristischen Zahlen aus dem Jahr 1679 sind ein arithmetisches Modell der Logik des Aristoteles. Seinen Hauptkalkül entwickelte er in den Generales Inquisitiones von 1686. Er entwarf dort die erste Gleichungslogik und leitete in ihr fast zwei Jahrhunderte vor der Boole-Schule die Gesetze der booleschen Verbandsordnung ab. Innerhalb dieses Kalküls formulierte er die traditionelle Begriffslogik bzw. Syllogistik auf gleichungslogischer Grundlage. Er erfand die Mengendiagramme lange vor Leonhard Euler und John Venn und stellte mit ihnen die Syllogistik dar. Das Leibniz'sche Gesetz geht auf ihn zurück. Während eines Parisaufenthalts in den Jahren 1672 bis 1676 trat Leibniz in Kontakt zu führenden Mathematikern seiner Zeit. Ohne sichere theoretische Grundlage lernte man damals, unendliche Folgen und Reihen aufzusummieren. Leibniz fand ein Kriterium zur Konvergenz alternierender Reihen (Leibniz-Kriterium), aus dem insbesondere die Konvergenz der sogenannten Leibniz-Reihe. Durch Summation von Reihen gelangte Leibniz 1675 zur Integral- und von dort zur Differentialrechnung. Er dokumentierte seine Erfindung 1684 mit einer Veröffentlichung in den acta eruditorum. Von Gottfried Wilhelm Leibniz stammen auch die nachfolgende Reihen für π, die er bei der Untersuchung des Konvergenzverhaltens unendlicher Reihen 1673 fand. |
|
| Die einfache, aber nur sehr langsam konvergierende obere Formel lässt sich mit Hilfe der Potenzreihe des Arcustangens ableiten. |
| Abraham
Sharp (1653 - 18. Juli 1742) war ein englischer
Astronom, Mathematiker und Instrumentenbauer. Bis zum Ende seines Lebens lebte er in Horton Hall, baute Instrumente, korrespondierte mit zahlreichen Wissenschaftlern und führte Berechnungen aus. Einen Schwerpunkt bildete die Zusammenarbeit mit seinem früheren Arbeitgeber Flamsteed. Die sich daraus ergebende Korrespondenz ist weitgehend erhalten. Unter anderem baute er für Flamsteed ein Mikrometer (1704), berechnete Positionen des Mondes und der Planeten sowie umfangreiche Tabellen für die Historia coelestis und erstellte Finsternistabellen der Jupitermonde. Nach Flamsteeds Tod korrespondierte er mit dessen Assistenten Joseph Crosthwait, half bei der Neuausgabe der Historia coelestis Britannica (1725) und fertigte Sternkarten für den Atlas coelestis (1729). Abraham Sharp berechnet 1699 mit Hilfe der Arcustangens-Reihe von Gregory und Leipniz 72 Stellen von π. |
| John Machin (1680 - 9. Juni 1751) war ein Astronom und Mathematiker mit einer Professur am Gresham College in London. Er ist bekannt wegen seiner 1706 entdeckten arctan-Formel für die Kreiszahl π. |
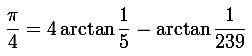 |
| Seine
Gleichung lässt sich zusammen mit der taylorschen
Reihenentwicklung der Arcustangens-Funktion für schnelle
Berechnungen verwenden. John Machin berechnete mit seiner
Formel von 1706 die ersten 100 Stellen von π. Erst 1958 publizierte G.F. Freeman (Math. Gazette 42, S.285) folgende noch schneller konvergierende Formel: |
 |
| Georg
Freiherr von Vega (23. März 1754 - 26. September 1802) war
ein österreichischer Mathematiker und
Artillerieoffizier. Sein für die Technik wichtigstes
Werk sind die 7-stelligen Logarithmentafeln und deren
Neuausgabe als „Vega-Bremiker“. Zu einem Bestseller wurde auch Vegas 4-bändiges Lehrbuch Vorlesungen über die Mathematik (1782-1800), eines davon über sogenannte „Einfache Maschinen“). Zu erwähnen sind noch Publikationen zur Zeitmessung und zu einem System der Maßeinheiten, die in den letzten Lebensjahren entstanden. 1789 stellte Vega einen neuen Rechenrekord auf, indem er die Kreiszahl π auf 140 Stellen berechnete (wovon sich später 126 als richtig herausstellten). Dieser Rekord hielt mehrere Jahrzehnte. Bei seiner Berechnung stellte Vega fest dass De Lagny nur 112 richtige Stellen gefunden hatte. |
| Der griechische Buchstaben
’π’ (p) zur Bezeichnung der
Verhältniszahl des Kreisumfangs um Kreisdurchmesser soll
sich ableiten aus dem griechischen Wort perijeria
(periphereia) = Kreis(umfang), Umkreis, Umfangslinie oder
auch von perimetros, dt. Umfang. Der griechische Buchstabe π wurde als Abkürzung für "Peripherie" von englischen Mathematikern benutzt. William OughtredWilliam Oughtred (5. März 1574 - 30. Juni 1660) war ein englischer Mathematiker. Bekannt wurde William Oughtred durch die Erfindung des Rechenschiebers im Jahre 1622 (nach anderen Quellen 1621). Ferner führte er 1631 das mathematische Symbol „ד für Multiplikationen und „/“ für Divisionen ein.Ebenso bezeichnete Oughtred in seiner Schrift Theorematum in libris Archimedis de Sphaera et Cylindro Declaratio als erster Mathematiker die Kreiszahl mit „π“ um das Verhältnis von halbem Kreisumfang (semiperipheria) zu Halbmesser (semidiameter) auszudrücken Isaac BarrowIssac Barrow wurde im Oktober 1630 in London als Sohn von Thomas Barrow geboren. Bekannt ist er vor allem als Lehrer von Isaac Newton. Er gab durch eine Methode, mittels des charakteristischen Dreiecks, das erst später von Leibniz so genannt wurde, Tangenten an Kurven zu ziehen, die erste Veranlassung zur Differentialrechnung. Er erkannte früh, dass die Integralrechnung und die Differentialrechnung zueinander invers sind. Er hatte maßgeblichen Anteil an der Reihenentwicklung.und benutzte dieselben Bezeichnungen wie William Oughtred und Isaac Barrow für π, etwa um 1664. William JonesWilliam Jones (1675 - 1. Juli 1749) war ein walisischer Mathematiker. Obwohl Jones keine Universität besucht hatte und keine Beiträge zur mathematischen Forschung erbrachte, stand er mit einigen herausragenden Mathematikern seiner Zeit in Kontakt, insbesondere mit Isaac Newton.Seit 1711 war Jones Mitglied der Royal Society. Für diese wurde er 1713 Mitglied einer Kommission, die den Prioritätsstreit zwischen Newton und Gottfried Wilhelm Leibniz klären sollte. Jones veröffentlichte auch ein Buch nach Newtons Notizen Analysis per quantitatum series, fluxiones, ac differentias: cum enumeratione linearum tertii ordinis, London 1711. In seinem Lehrbuch Synopsis palmariorum matheseos: or, A new introduction to the mathematics, London 1706, verwendete er das Symbol π (abgeleitet von engl. Perimeter „Umfang“). David GregoryDavid Gregory (3. Juni 1659 - 10. Oktober 1708) war Professor für Mathematik an der Universität Edinburgh und Professor für Astronomie an der Universität Oxford. Er war ein Kommentator zu den Philosophiae Naturalis Principia Mathematica von Isaac Newton.David Gregory verwendete 1697 die Bezeichnung π\&rho für das Verhältnis von Umfang zu Radius. |
| Leonhard Euler (15. April 1707
-7. Septemberjul./ 18. September 1783greg) war einer der
bedeutendsten Mathematiker. Insgesamt gibt es 866 Publikationen von ihm. Ein großer Teil der heutigen mathematischen Symbolik geht auf Euler zurück (z. B. e, π, i, Summenzeichen Sum, f(x) als Darstellung für eine Funktion). 1744 gab er ein Lehrbuch der Variationsrechnung heraus. Euler kann auch als der eigentliche Begründer der Analysis angesehen werden. 1748 publizierte er das Grundlagenwerk Introductio in analysin infinitorum, in dem zum ersten Mal der Begriff der Funktion die zentrale Rolle spielt. Am 3. September 1750 las Leonhard Euler vor der Berliner Akademie der Wissenschaften ein Mémoire, in dem er erneut das von Isaac Newton deklarierte Prinzip Kraft gleich Masse mal Beschleunigung vorstellte. In den Werken Institutiones calculi differentialis (1765) und Institutiones calculi integralis (1768–1770) beschäftigte er sich außer mit der Differential- und Integralrechnung unter anderem mit Differenzengleichungen, elliptischen Integralen sowie auch mit der Theorie der Gamma- und Betafunktion. Andere Arbeiten setzen sich mit Zahlentheorie, Algebra (z. B. Vollständige Anleitung zur Algebra, 1770), angewandter Mathematik (z. B. Mechanica, sive motus scientia analytica exposita, 1736 und Theoria motus corporum solidorum seu rigidorum, 1765) und sogar mit der Anwendung mathematischer Methoden in den Sozial- und Wirtschaftswissenschaften auseinander (z. B. Rentenrechnung, Lotterien, Lebenserwartung). In der Mechanik arbeitete er auf den Gebieten der Hydrodynamik (Eulersche Bewegungsgleichung, Turbinengleichung) und der Kreiseltheorie (Eulersche Kreiselgleichungen). Die erste analytische Beschreibung der Knickung eines mit einer Druckkraft belasteten Stabes geht auf Euler zurück. Er begründete damit die Stabilitätstheorie. In der Optik veröffentlichte er Werke zur Wellentheorie des Lichts und zur Berechnung von optischen Linsen zur Vermeidung von Farbfehlern. Seine 1736 veröffentlichte Arbeit Solutio problematis ad geometriam situs pertinentis beschäftigt sich mit dem Königsberger Brückenproblem und gilt als eine der ersten Arbeiten auf dem Gebiet der Graphentheorie. Ausgangspunkt für die weiteren Untersuchungen der Kreiszahl waren einige grundlegende Erkenntnisse Leonhard Eulers, die dieser 1748 in seinem Werk Introductio in analysin infinitorum veröffentlicht hatte. Euler stellte unter anderem mit der bekannten Formel eiz
= cos z + i·sin z
|

|
| Leonhard Euler schaffte mittels Bleistift und Papier in einer Stunde 20 Dezimalen von π. Aufgegriffen wurde der Buchstabe später von Leonhard Euler in seiner Abhandlung „Variae observationes circa series infinitas“. Euler verwendet zunächst p bis 1735, ab 1738 dann π. Danach etablierte sich der griechische Buchstabe auch bei anderen Mathematikern als Symbol für die Kreiskonstante und setzte sich so dann überall durch. |
| Johann Heinrich Lambert (26. August 1728 -
25. September 1777) war ein schweizerisch-elsässischer
Mathematiker, Logiker, Physiker und Philosoph der
Aufklärung. Lambert gehörte zu den hervorragendsten Mathematikern und Logikern seiner Zeit. Die Lehre von Intensitätsmessung des Lichts begründete er als Wissenschaft in seinem Werk Photometria, seu de mensura et gradibus luminis colorum et umbras (Augsburg 1760). Weiterhin erforschte er – selbst seit seiner Geburt schwerhörig – die Theorie des Sprachrohrs. Vor allem in der Photometria, aber auch in seinem Buch Beyträge zum Gebrauche der Mathematik und deren Anwendung (Vol. 1, 1765), verknüpfte er Ideen von Thomas Simpson, Rugjer Josip Boškovic und Mayer. Seine Arbeit in der Photometrie und Geodäsie führte ihn zu einer allgemeinen Theorie der Fehler. Er diskutierte das Problem der Anwendung von Wahrscheinlichkeitsverteilungen auf Fehlerterme und verwendete bereits eine Maximum-Likelihood-Methode für die Bestimmung von Mittelwerten. Außerdem erwarb sich der aufgeklärte Gelehrte Verdienste um die Erkenntnistheorie, der er sein Werk Neues Organon, oder Gedanken über die Erforschung und Bezeichnung des Wahren (2 Bde., Leipzig 1764) widmete. 1761 (im Druck 1768) wies Lambert die Irrationalität der Kreiszahl π mit Hilfe der Theorie der Kettenbrüche nach. Er vermutete ferner, dass e und π transzendente Zahlen sind. |
| Irrationalität einer Zahl besagt,
das sie nicht als Bruch zweier ganzen Zahlen darstellbar
ist. Lambert nähert sich der Kreiszahl durch eine Folge
von Brüchen. Zuerst zeigte er, daß tan x nicht rational sein kann, wenn Daraus folgerte er, daß x nicht rational sein kann, wenn tan x rational ist wie dies z.B. in dem Ausdruck tan π/4 = 1 der Fall ist. Daraus schloß Lambert, das π/4 und damit auch π nicht rational sein können. Mit Hilfe von Kettenbrüchen konnte er auch die besten Näherungen in Form von Brüchen berechnen. Dazu zählt beispielsweise: |
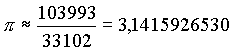
|
| Diese Vorarbeit machte sich Johann Heinrich Lambert zunutze, der mit Hilfe einer der eulerschen Kettenbruchentwicklungen 1766 erstmals zeigen konnte, dass e und π irrationale, also nicht durch einen ganzzahligen Bruch darstellbare Zahlen sind. |
| Adrien-Marie Legendre (18. September
1752- 10. Januar 1833) war ein französischer
Mathematiker. Legendre leistete wichtige Beiträge auf den unterschiedlichsten Gebieten der Mathematik, wurde allerdings schon zu Lebzeiten von denen des 25 Jahre jüngeren Carl Friedrich Gauß in den Schatten gestellt, der in merkwürdiger Parallelität (Felix Klein) auf fast denselben Gebieten wie Legendre arbeitete, häufig aber tiefer vordrang. So entdeckte Legendre vor Gauß 1806 die Methode der kleinsten Quadrate, die er ebenfalls in der Astronomie benutzte (bei der Bestimmung der Kometenbahnen aus drei Beobachtungen), und fand auch vor Gauß das Quadratische Reziprozitätsgesetz (das allerdings schon Euler in Arbeiten von 1751 und 1783 kannte), dessen erste Beweise von Gauß stammen. Der Begriff Legendre-Symbol in der Zahlentheorie erinnert noch heute an die Leistungen Legendres bei dessen Formulierung. Legendre anerkannte die Beiträge von Gauß und berücksichtigt sie auch in der stark überarbeiteten zweiten Auflage seiner Zahlentheorie von 1808, beklagte sich aber gleichzeitig bitter darüber, dass Gauß umgekehrt alle Prioritäten für sich in Anspruch nahm. Auch die asymptotische Formel für die Primzahlverteilung findet sich in Legendres Zahlentheorie von 1798. Sie steht am Anfang der Verwendung analytischer Methoden in der Zahlentheorie. In der Analysis ist Legendre nicht nur für seine Legendre-Polynome in der Potentialtheorie bekannt, sondern auch für seine Arbeiten über elliptische Integrale, in der seine Einteilung in drei „Gattungen“ nach ihm benannt ist. Er behandelte sie zusammen mit anderen über Integrale definierten Funktionen wie der Gammafunktion und der Betafunktion in seinen Exercises du calcul integral, die in drei Bänden 1811, 1817, 1819 erschienen. In der Mechanik ist Legendre auch für die Legendre-Transformation bekannt. Eine kleine Lücke in Lamberts Beweisführung wurde 1806 von Adrien-Marie Legendre geschlossen, der gleichzeitig den Irrationalitätsbeweis für π/2 erbrachte. |
| Johann Carl Friedrich Gauß
(30. April 1777 -
23. Februar 1855) war ein deutscher Mathematiker,
Statistiker, Astronom, Geodät und Physiker. Wegen seiner
überragenden mathematischen und naturwissenschaftlichen
Leistungen galt er bereits zu seinen Lebzeiten als
„Fürst der Mathematiker“. Einige Anekdoten besagen, dass er bereits als dreijähriger seinen Vater bei der Lohnabrechnung korrigiert haneb soll. Später sagte Gauß von sich selbst, er habe das Rechnen schon vor dem Sprechen gelernt. Sein Leben lang behielt er die Gabe, selbst komplizierteste Rechnungen im Kopf durchführen zu können. Als der „Wunderknabe“ Gauß vierzehn Jahre alt war, wurde der Herzog Karl Wilhelm Ferdinand von Braunschweig aufmerksam auf ihn und unterstützte ihn finanziell. So konnte Gauß von 1792 bis 1795 am Collegium Carolinum studieren. Mit 18 Jahren entwickelte Gauß die Grundlagen der modernen Ausgleichungsrechnung und der mathematischen Statistik (Methode der kleinsten Quadrate), mit der er 1801 die Wiederentdeckung des ersten Asteroiden Ceres ermöglichte. Auf Gauß gehen die folgenden Arbeiten zurück: Begründung und Beiträge zur nicht-euklidischen Geometrie, Primzahlverteilung und Methode der kleinsten Quadrate, Einführung der elliptischen Funktionen, Fundamentalsatz der Algebra, Beiträge zur Verwendung komplexer Zahlen, Beiträge zur Zahlentheorie, Beiträge zur Astronomie, Beiträge zur Potentialtheorie, Landvermessung und Erfindung des Heliotrops, Gaußsche Krümmung und Geodäsie, Magnetismus, Elektrizität und Telegrafie |
 |
| Joseph Liouville (24. März 1809 -
8. September 1882) war ein französischer Mathematiker. Liouville arbeitete in zahlreichen mathematischen Teilgebieten, darunter Zahlentheorie, Funktionentheorie und Differentialgeometrie, aber auch in mathematischer Physik und sogar in Astronomie. Ein bekanntes Ergebnis ist der Satz von Liouville, an dem heute keine Einführung in die Funktionentheorie vorbeikommt. Liouville war auch der erste, dem ein Beweis für die Existenz transzendenter Zahlen gelang, indem er eine unendliche Klasse solcher Zahlen als Kettenbrüche konstruierte (Liouville-Zahlen). Er führte auch eine zahlentheoretische Funktion, die Liouville-Funktion ein. Weiter zeigte Liouville, dass die Stammfunktion elementarer Funktionen nicht elementar sein muss. Die Vermutung, dass π nicht algebraisch sein könne, stand nach Lamberts Beweis der Irrationalität jetzt im Raum, wurde zumindest von Euler, Lambert und Legendre ausgesprochen. Dabei war bis zur Mitte des 19. Jahrhundert noch nicht klar, dass es überhaupt transzendente Zahlen geben musste. Dieser Nachweis gelang 1844/1851 Joseph Liouville durch explizite Konstruktion von transzendenten liouvilleschen Zahlen. |
| Charles Hermite (24. Dezember 1822
- 14. Januar 1901) war ein französischer Mathematiker. Hermite arbeitete in Zahlentheorie und Algebra, über orthogonale Polynome und elliptische Funktionen. Er erzielte wichtige Ergebnisse über doppelt periodische Funktionen und Invarianten quadratischer Formen. 1858 löste er eine algebraische Gleichung fünften Grades mit Hilfe elliptischer Funktionen. 1873 erzielte er sein wohl berühmtestes Resultat: Er bewies, dass die eulersche Zahl e transzendent ist; auf Hermites Methode aufbauend bewies Carl Louis Ferdinand von Lindemann 1882 die Transzendenz der Kreiszahl π (Unmöglichkeit der Quadratur des Kreises durch Zirkel und Lineal. |
| Ferdinand von Lindemann
(12. April 1852 -
6. März 1939) war ein deutscher Mathematiker. Aus dieser Zeit (1882) stammt sein Beweis, dass die Kreiszahl π eine transzendente Zahl ist (siehe Satz von Lindemann-Weierstraß); daraus folgte erstmals ein Beweis für die Unmöglichkeit der Quadratur des Kreises mittels Zirkel und Lineal. Lindemann griff in seiner Arbeit auf ein Ergebnis des französischen Mathematikers Charles Hermite zurück. Dieser hatte 1873 gezeigt, dass die eulersche Zahl e transzendent ist. Lindemann (1852-1939) bewies dann im Jahre 1882, das π eine transzendente Zah ist, d.h. unter anderem: π ist unendlich und unperiodisch. |
Unendlichkeit und Unperiodizität langen allein allerdings nicht aus, um Transzendenz einer Zahl zu gewährleisten. Transzendenz einer Zahl bedeutet: Nicht Lösung einer Gleichung mit GANZZAHLIGEN oder RATIONALEN Koeffizienten zu sein. Den Beweis veröffentlichte er in dem Artikel "Über die Zahl π" in den "Mathematischen Annalen" in München. Zuerst bewies Lindemann, daß die Lösung von eip + 1 = 0 nicht algebraisch sein kann. Er wußte aber, daß π dieser Gleichung genügte (das hatte schon Newton bewiesen), woraus er noch weiter folgerte, daß π keine algebraische Zahl sein kann. Die Konsequenz ist, das eine Konstruktion der Zahl π durch Lineal und Zirkel, also die geometrische Quadratur des Kreises nicht exakt möglich ist. Zu erwähnen wäre da noch das, seit den Griechen, quasi ganze Generationen von Mathematikern vorher versucht hatten, eine Lösung der Quadratur mit Zirkel und Lineal zu erreichen. Lindemanns Beweis zeigt demzufolge auch die Aussichtslosigkeit eines solchen Unterfangens. Was andererseits bedeutet, das vorhandene geometrische Konstruktionen, die Quadratur des Kreises betreffend, als Näherungslösungen zu betrachten sind. Und bei Näherungen, das heißt bei ihrer Anwendung und Benutzung, spielt eher die Frage der Genauigkeit eine grosse Rolle. |
| David Hilbert (23. Januar 1862
-14. Februar 1943) war ein deutscher Mathematiker. Er
gilt als einer der bedeutendsten Mathematiker der
Neuzeit. Viele seiner Arbeiten auf dem Gebiet der
Mathematik und mathematischen Physik begründeten
eigenständige Forschungsgebiete. Seine Vorschläge zu den Grundlagen der Mathematik veranlassten eine kritische Analyse der Begriffsdefinitionen der Mathematik und des mathematischen Beweises. Diese Analysen führten zum Gödelschen Unvollständigkeitssatz, der unter anderem zeigt, dass das sogenannte „Hilbertprogramm“ nicht erfüllt werden kann. Hilberts programmatische Rede auf dem internationalen Mathematikerkongress in Paris im Jahre 1900, in der er eine Liste von 23 mathematischen Problemen vorstellte, beeinflusste die mathematische Forschung des 20. Jahrhunderts nachhaltig. Lindemanns Beweis für die Transzendenz von π wurde in den folgenden Jahren und Jahrzehnten noch wesentlich vereinfacht, so etwa durch David Hilbert im Jahre 1893. |
| Srinivasa Ramanujan Aiyangar (22. Dezember 1887
- 26. April 1920) war ein indischer Mathematiker. Er ist
vor allem dafür bekannt, sich all sein Wissen
autodidaktisch beigebracht zu haben. Von 1914 bis 1919
arbeitete er gemeinsam mit dem britischen Mathematiker
Godfrey Harold Hardy am Trinity College der Universität
Cambridge in England. Während dieser Zeit wurden ihm
zahlreiche Ehrungen und Auszeichnungen zuteil. Ramanujans
mathematischer Nachlass tauchte erst 1976 wieder auf und
besteht aus über 600 Formeln und Sätzen, von denen
einige bis heute nicht vollständig bewiesen sind. Ramanujan beschäftigte sich während der fünf Jahre in England (1914-1919) hauptsächlich mit der Zahlentheorie. Dabei wurde er durch viele Summenformeln, die Konstanten wie die Kreiszahl π, Primzahlen und Partitionsfunktionen enthalten, berühmt. Zudem erstellte er eine sehr gute Näherungsformel für die Berechnung des Ellipsenumfangs. Bekannt wurde auch seine Kettenbruchentwicklung, die er noch 1914 veröffentlichte und mit deren Hilfe man in nur zehn Schritten 88 Stellen von π errechnen kann. 1985 gelang es Bill Gosper auf diese Weise, π auf 17.000.000 Stellen hinter dem Komma auszurechnen. Insgesamt fand Ramanujan in Cambridge etwa 3.900 mathematische Resultate, in der Mehrzahl Identitäten und Gleichungen, von denen die meisten im Nachhinein bewiesen werden konnten. |
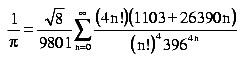 |
| Im Jahr 1913 erschien eine geometrische Konstruktion von Ramanujan, die ebenfalls auf der Näherung π = 335/113 beruht. Siehe dazu: Näherungskonstruktion Ramanujan |
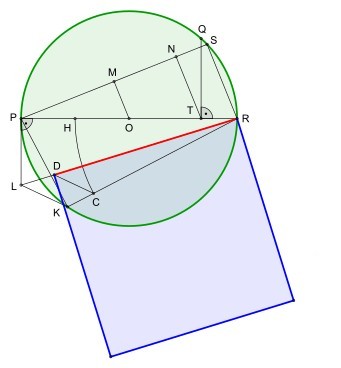
Jacob de Gelder1849 erschien in Grünerts Archiv eine einfache Konstruktion von Jacob de Gelder (1765–1848). Das war 64 Jahre früher, als die Veröffentlichung der vergleichbaren Konstruktion von S. A. Ramanujan. Siehe dazu: Näherungskonstruktion Jacob de Gelder |
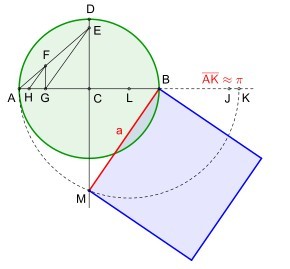
E. W. HobsonEine einfache und gut nachvollziehbare Konstruktion stammt von E. W. Hobson aus dem Jahr 1913. Sie benötigt für die Seite des Quadrates nur drei Halbkreise und zwei zueinander rechtwinklig stehende Strecken. Siehe dazu: Näherungskonstruktion Hobson |
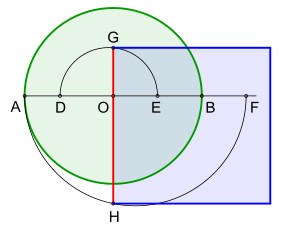
Louis LoynesEine Methode veröffentlichte Louis Loynes 1961. Sie beruht auf der Feststellung, dass der Flächeninhalt des Umkreises eines rechtwinkligen Dreiecks gleich dem Quadrat über der größeren Kathete ist, wenn der Tangens des kleineren Winkels, also das Verhältnis von kleinerer zu größerer Kathete. Siehe dazu: Näherungskonstruktion Louis Loynes |
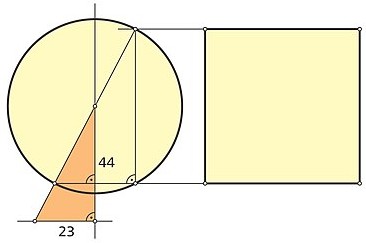
| David Harold Bailey (14. August 1948)
ist ein US-amerikanischer Mathematiker und Informatiker.
Zusammen mit Peter Borwein und Simon Plouffe wurde er
1996 durch die Veröffentlichung der BBP-Reihe
für π bekannt. Diese Reihe wurde mit Hilfe des PSLQ-Algorithmus für die Auffindung einer ganzzahligen linearen Abhängigkeit (Ganzzahlbeziehung) vorgegebener reeller Zahlen entdeckt. Der PSLQ Algorithmus wurde 1992 durch Bailey und Helaman Ferguson entwickelt. Peter Benjamin Borwein (5. Oktober 1953) ist ein kanadischer Mathematiker, der als Mit-Entdecker der Bailey-Borwein-Plouffe-Formel (nach D. Bailey, P. Borwein und S. Plouffe) zur Berechnung einer beliebigen hexadezimalen Stelle von π (ohne Kenntnis vorheriger Ziffern) bekannt wurde. Er ist als Vertreter der Experimentellen Mathematik bekannt. Simon Plouffe (11. Juni 1956) ist ein kanadischer Mathematiker. 1996 entdeckte David Harold Bailey, zusammen mit Peter Borwein und Simon Plouffe, diese neuartige Reihendarstellung (BBP-Reihe ) für π: |
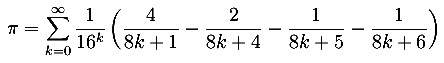 |
| Johann Martin Zacharias Dase (23. Juni 1824 -
11. September 1861) war ein deutscher Schnellrechner und
Rechenkünstler. Dase zeigte schon in seiner Jugend eine leidenschaftliche Vorliebe für das Rechnen und widmete der Übung darin fast jede freie Stunde. Seit 1839 trat er in Deutschland, Österreich und England als Rechenkünstler auf. So multiplizierte er in Wien eine 40ziffrige Zahl mit einer anderen 40ziffrigen in 40 Minuten, in Wiesbaden eine 60ziffrige mit einer anderen 60ziffrigen in 2 Stunden 59 Minuten bei lebhafter Unterhaltung der Gesellschaft und zog in München die Quadratwurzel aus einer 60ziffrigen Zahl in 20 Minuten und eine aus einer 100ziffrigen in 52 Minuten. In sechs Stunden intensiven Kopfrechnens erkannte er die Repunitzahl R11 als zusammengesetzte Zahl. Auf Empfehlung von C.F. Gauß fand er später eine Anstellung, bei der er Tafeln für Logarithmen- und Hyperbelfunktionen berechnete Johann Dase verwendete 2 Monate seines Lebens darauf, 200 Stellen der Zahl π zu berechnen. 1837 J. F. Callet veröffentlicht in Paris 152 Stellen. 1841 William Rutherford bestimmt 208 Stellen. 1847 Thomas Clausen findet mit Hilfe der Machinschen und Eulerschen Formeln 248 Nachkommastellen. 1853 Rutherford zieht mit 440 Stellen nach. 1853 William Shanks übertrifft Rutherford noch im selben Jahr mit 707 Stellen. Später fand man aber heraus, daß er sich ab der 528. Stelle verrechnet hatte. 1945 wies Ferguson den Fehler in Shanks' Berechnungen mit Hilfe eines "Tischrechners" nach. 1949 rechnete ENIAC neunzig Stunden lang an den ersten 2037 Stellen von π Am 29. Juli 1961 wurden auf einer IBM 7090 in New York 100 265 Dezimalstellen von π in 8 Stundenberechnet. 1967 berechnete der französische Computer CDC 6600 500 000 Stellen von π . 1988 waren es bereits 16777216 Stellen, die Yoshiaki Tamura und Tasumasa Kanada mit einem Computer berechneten. Zur Zeit sind mehr als 1 Milliarde Stellen von π bekannt. Eine Tabelle zur Entwicklung der Stellenzahl von π: |
| Mathematiker | Jahr | berechnete Stellen |
|---|---|---|
| Vieta | 1580 | 10 |
| van Roomen | um 1600 | 15 |
| van Ceulen | um 1605 | 35 |
| Abraham Sharp (1651-1742) | 1706 | 72 |
| John Machin | 1707 | 100 |
| Thomas de Lagny | 1719 | 127 |
| Georg von Vega(1756-1802) | 1793 | 140 |
| Thibaut | 1822 | 156 |
| William Rutherford | 1841 | 208 |
| Zacharias Dase | 1844 | 200 |
| Thomas Clausen(1801-1885) | 1847 | 248 |
| William Rutherford | 1853 | 440 |
| Prof. Richter (Elbing) | 1855 | 500 |
| William Shanks (GB) | 1874 | 707 |
| D. F. Ferguson (GB) | 1946 | 730 |
| John W. Wrench Jr. und Levi B. Smith | 1947 | 808 |
| G. W. Reitwieser (USA) auf ENIAC | 1949 | 2 035 |
| S. C. Nicholson und J. Jeenel auf NORC | 1954 | 3 089 |
| Felton auf Pegasus | 1958 | 10 000 |
| F. Genuis (Paris) auf IBM 704 | 1958 | 10 000 |
| J. M. Gerard (London) auf IBM 7090 | 1961 | 20 000 |
| Daniel Shanks und John W. Wrench Jr. auf IBM 7090 | 1961 | 100 265 |
| Guilloud und Bouyer auf CDC 7600 | 1973 | 1 000 000 |
| Yoshiaki Tamura und Yasuma Kanada (Japan) auf HITAC M-280H | 1983 | 16777216 |
| Gosper auf Symbolics | 1985 | 17 000 000 |
| D. H. Bailey auf Cray-2 | 1986 | 29 360 000 |
| Kanada auf SX 2 | 1987 | 134217728 |
| Kanada | 1988 | 201 326 000 |
| Kanada auf HITAC S-820/80 | 1989 | 1 073 740 000 |