 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 8.2.0 | Der Gizeh-Komplex und die Quadraturwinkel | |
| 8.2.1 | Die Quadratur 2 und die Chefren-Pyramide | |
| 8.2.2 | Die Quadratur 1 und der Sphinx | |
| 8.2.3 | Die gesamte Quadratur im Gizeh-Komplex | |
|
| 8.2.0 | Der Gizeh-Komplex und die Quadraturwinkel |
 |
 |
 |
| Schneidet man die Cheopspyramide in
Nord-Süd oder Ost-West-Richtung durch, so erhält man
als Schnittfigur ein Quadraturdreieck. Damit erhebt sich die Frage, ob die Quadratur des Kreises auch im gesamten Gizeh-Komplex vorhanden ist. |
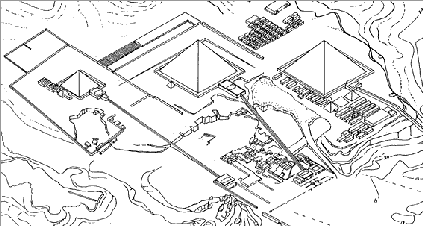
| Die Quadratur des Kreises als Näherung
liefert zwei Winkel (Quadratur 1+2). Trägt man diese
Winkel an die Cheops-Pyramide an, so ergibt sich das
nebenstehende Bild. Deutlich ist zu erkennen, dass der
Sphinx genau zwischen den beiden Schenkeln der Winkel
liegt. |
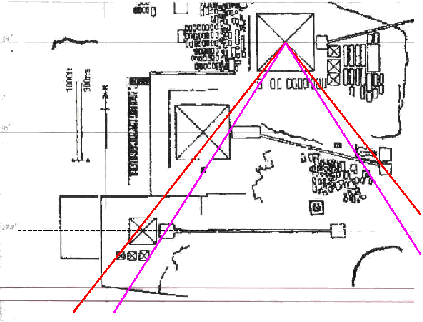
| Bemerkung: Die Karten des Gizeh-Komplexes, die man
erhalten kann, lassen sich in zwei Kategorien einteilen.
In topographisch orientierte und in magnetisch
orientierte Karten. Die Differenz beider Karten
zueinander besteht in einer Drehung von etwa 1 Grad. Je nach Karte (topographisch/magnetisch) kann der Mittelpunkt der Mykerinos-Pyramide einmal knapp unterhalb und einmal knapp oberhalb des 14:11-Schenkels liegen !!! |
| 8.2.1 | Die Quadratur 2 und die Chefren-Pyramide |
|
|
|
| Durch die eingezeichneten Breiten- und Längengrade der Pyramiden und durch die Schenkel der Winkel kann man für die Chefren-Pyramide sofort die Quadraturkonstruktion 2 erzeugen. |
| 8.2.2 | Die Quadratur 1 und der Sphinx |
|
|
|
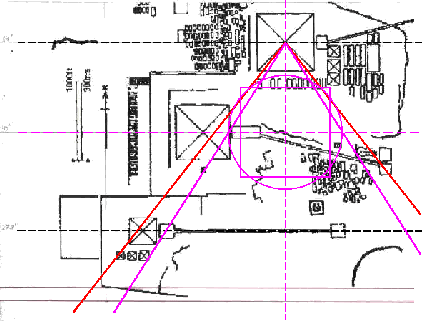
| Das Quadraturdreieck
2 (magenta) hat die Proprtion 11:7. Die Strecke
Cheops-Chefren-Pyramide kann man daher in 11 Einheiten
zerlegen. Daraus lässt sich die Quadratur 1 gewinnen, indem diese Strecke auf 14 Einheiten verlängert wird. Durch Einzeichnen der Grundseite (waagerechte rote Linie) erhält man dann sofort das Quadraturdreieck 1 |
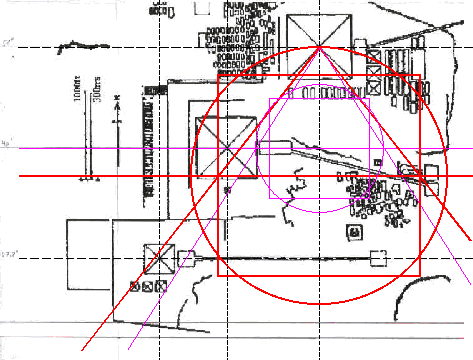
| Deutlich ist zu erkennen, dass der Sphinx genau in der rechten Ecke des roten Dreiecks liegt. Zufall ? |
| 8.2.3 | Die gesamte Quadratur im Gizeh-Komplex |
|
|
|
| Trägt man die gesamte Quadratur, mit den
entsprechenden In- und Umkeisen bzw. In-und Umquadraten (Erweiterungen 1) in den
Gizeh-Komplex ein, so ergibt sich das nebenstehende Bild. Aus der Abbildung lässt sich eigentlich nur eine Konsequenz ziehen: |
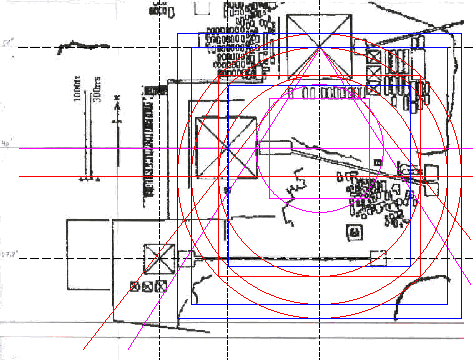
Die Quadratur des Kreises, also die geometrische Konstruktion der Näherung, war den Ägyptern durchaus bekannt. Dies sagt allerdings noch gar nichts darüber aus, ob die Ägypter den tatsächlichen Wert von π kannten. |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
