DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 9.1.0 | Der Ausgangspunkt in Bottrop | |
| 9.1.1 | Der Punkt in Essen | |
| 9.1.2 | Die Grundlinie Bottrop-Essen | |
| 9.1.3 | Die Quadratur im Ruhrgebiet | |
| Steht man im Bottroper Stadtgarten auf der großen Wiese zwischen Overbeckshof und dem Marienhospital, etwa 100 m vom Ausgang zur Josef-Albers-Sraße entfernt, so befindet sich dort ein "ausgezeichneter" geographischer Punkt. Landschaftsmäßig ist dieser Punkt allerdings gar nicht weiter auffällig, da lediglich durch eine Buschgruppe markiert. |

| Die Abbildung zeigt einen Teil des
Stadtgartens vom Overbeckshof aus gesehen, mit Blick auf
die sogenannte Festwiese und dem Marienhospital. Etwa 100 Meter, etwas links hinter der Wasserfontäne, kann man im Hintergrund die erwähnte Buschgruppe gerade noch erkennen. Siehe dazu: Zwei besondere Punkte im Stadtpark Bottrop |
 |
Dieser Punkt und der nähere Bereich um ihn
(Kreis von etwa 20m Radius), ist in zweifacher Hinsicht,
ein zentraler Orientierungspunkt. 1) Er ist der
Mittelpunkt der unmittelbaren Lanschaftsstruktur in einem
Umfeld von 1 km. |
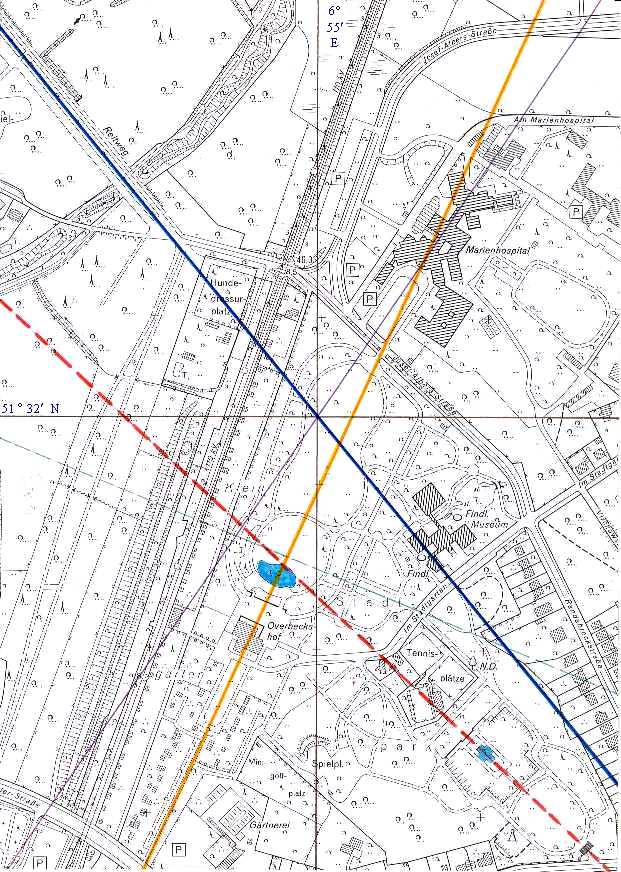 |
Der Stadtgarten vergrößert aber ohne die Stadtteiche. |
| Hinzu kommt, daß sich hier sowohl lokale wie regionale Ordnungsstrukturen überlappen. Denn gleichzeitig ist dies auch ein wichtiger Orientierungspunkt für die Landschaft im Umkreis von etwa 30 km. Das entspricht dem gesamten nordwestlichen Bereich des Ruhrgebietes. |
| Anhand der Baudaten von Kirchen,
Schlössern, Burgen und Häusern läßt sich zudem noch
zeigen, das die (damit verbundene) Geometrie der
Gesamtanlage, in den lezten 10 Jahrhunderten auch benutzt
worden ist. Die geographische Besonderheit dieses Punktes besteht darin, das seine Koordinaten, also Länge und Breite, keine Sekundenanteile enthalten. In "Knaurs Weltatlas" als geographische Position von Bottrop angegeben. Das galt offiziell bis zur kommunalen Neuordnung. Anhand der topographischen Karte 4407 (Bottrop) lassen sich die geographischen Koordinaten dieses Punktes ermitteln. |
| Phi | 51° 32´ N | geographische Breite |
| Lambda | 06° 55´ E | geographische Länge |
| Durch die topographische Karte 4508 (Essen) lassen sich die geographischen Daten des Münsters ermitteln. Der gesamte Komplex des Essener Doms erstreckt sich über folgende Koordinatenstrecken: |
| Phi | 51° 27´ 24-26" N | geographische Breite |
| Lambda | 07° 00´ 49-52" E | geographische Länge |
 |
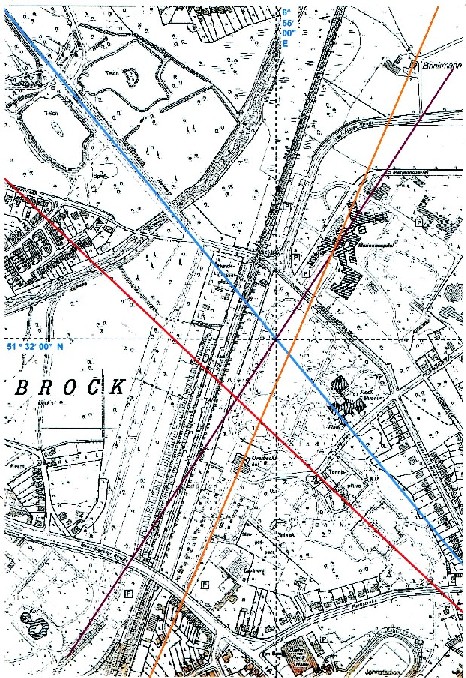
Die Verbindungslinie, vom Bottroper
Stadtgarten aus, führt zum Turm des St. Johann
Baptist-Teils, im vorderen Drittel des Doms. In der
Abbildung kann man den Turm in der linken oberen Ecke
deutlich erkennen. Betrachtet man den Turm von St. Johann Baptist auf der topographischen Karte, so erhält man die folgenden Koordinaten Siehe dazu: Das Essener Münster |
| Phi | 51° 27´ 25" N | geographische Breite |
| Lambda | 07° 00´ 50" E | geographische Länge |
| Nimmt man nun die Verbindungslinie vom Bottroper Stadtgarten zum Essener Dom, so ergibt sich mit dem Meridian durch Bottrop und dem Breitenkreis durch den Dom, ein rechtwinkliges Dreieck. In der folgenden Abbildung ist der gesamte Zusammenhang noch mal dargestellt. |
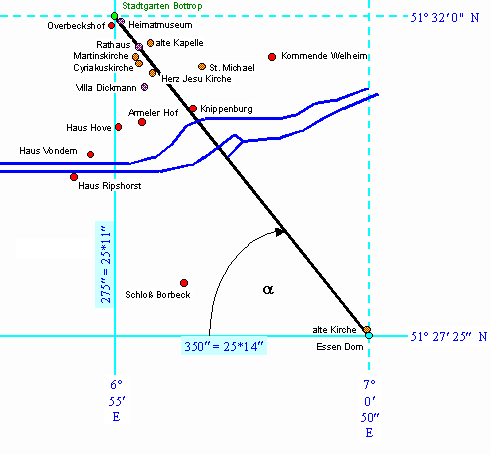 |
| Rein winkelmäßig gesehen lassen sich, aus den Ortskoordinaten, die Höhe und die Grundseite des Dreiecks aus der Abbildung bestimmen. |
| Die Höhe beläuft sich auf | 0° 4' 35'' | 275'' = 25 ·11 Bogensekunden |
| Die Basisseite besitzt eine Länge von | 0° 5' 50'' | 350'' = 25 ·14 Bogensekunden |
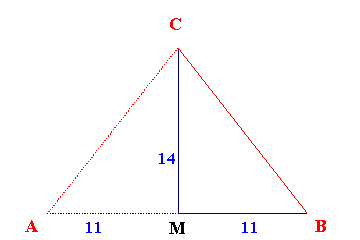 |
Der Tangens des Basiswinkels alpha
ergibt sich damit zu 11/14. Dies ist der sogenannte Quadraturwinkel, also der Winkel der bei der Konstruktion 1 der Quadratur des Kreises anfällt. Das entstandene Dreieck ist damit ein Schnittdreieck 1 und die Grundlinie ist (rechte) Seite des Quadraturdreicks 1 |
| Zu beachten ist, das die Spitze des Dreiecks
im Essener Dom liegt, wenn die Dreiecksseiten als
Winkel
behandelt werden. Nimmt man jedoch eine topographische
Karte und mißt dort den Winkel nach, so erhält man die
Dreiecksspitze in Bottrop. Spitzen- und Basiswinkel haben
ihre Plätze sozusagen vertauscht. Erklärbar wird dieses Phänomen, wenn man berücksichtigt, daß Breitenkreise einen vom Breitengrad abhängigen Radius besitzen. Am Äquator stimmen Breitenkreis und Erdumfang noch miteinander überein. Je weiter man sich aber vom Äquator in Richtung auf die Pole zu bewegt, um so kleiner wird der Umfang des Breitenkreises. Der Kosinus der geographischen Breite geht in den Umfang mit ein. Die Dreiecksseiten als Längen auf der Erdoberfläche können dann durchaus einen etwas differenten Winkel ergeben. |
| Die gesamte Quadratur des Kreises im Ruhrgebiet sieht dann so aus: |
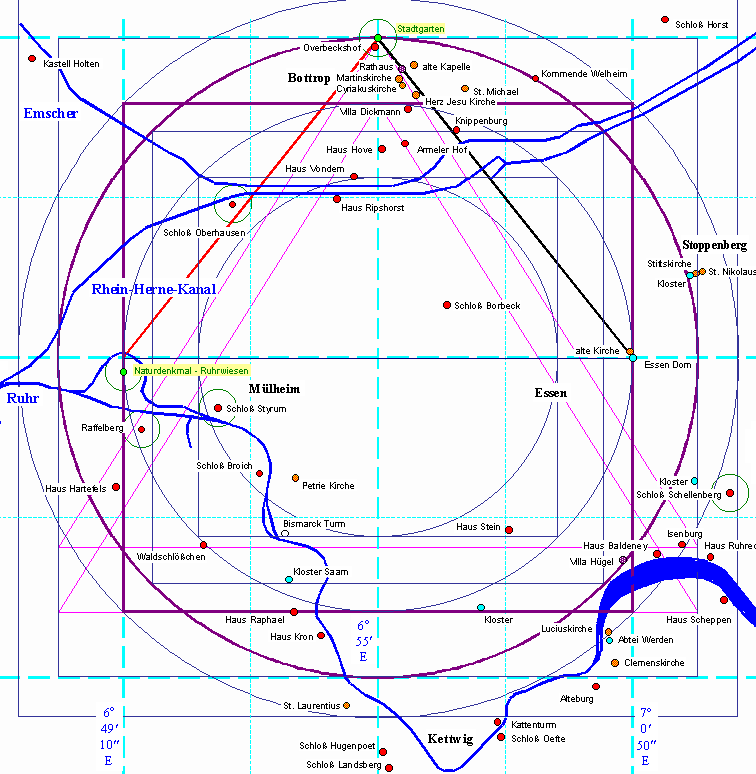 |
| Auf den Quadraten der
Quadratur liegen folgende Objekte: Knippenburg (1309/1340/50), Stiftskirche Stoppenberg (1073), Stift Rellinghausen (996), Haus/Kloster Schuir(.../1792), Haus Raphael, Kloster Saarn (1214), Naturdenkmal (Ruhrwiesen), Haus Vondern (1162) Auf den Kreisen
der Quadratur liegen folgende Objekte: |