1672 beobachtete der Astronom Jean Richer in Cayenne (Französisch-Guayana etwa +5 Grad nördliche Breite), das ein Sekundenpendel, das in Paris (etwa +49 Grad nördliche Bretie) durch die Länge justiert worden war, verkürzt werden mußte, um wieder Sekundenschwingungen zu erhalten. Das Pendelgesetz lautet ja folgendermaßen:

Isaac Newton und Christian Huygens entwickelten daraus physikalisch begründete Modelle der Erde, mit einer Abplattung an den Polen. Unter der Vorraussetzung eines homogenen, flüssigen und rotierenden Erdkörpers mit dem Schwerpunkt als Mittelpunkt, erhielt Newton 1687 einen Rotationsellipsoiden (siehe Abbildung 2) als Gestalt der Erde.

Die Oberfläche ergibt sich dabei als Gleichgewichtsfigur durch die Einwirkung der Gravitation und der Rotation der Erdmasse. Mit diesem Modell konnte Newton ein Anwachsen der Schwerebeschleunigung vom Äquator zu den Polen hin mit sin² φ postulieren.

φ ist dabei die geographische Breite, a die große Halbachse und b die kleine Halbachse der Erde. Für die Abplattung f erhielt er folgende Beziehung:

Der Physiker Christian Huygens, der unter anderem, 1657 die Pendeluhr und 1675 die Federuhr erfand, nahm 1690 als Ursprung der Erdanziehung den geometrischen Mittelpunkt der Erde, und erhielt eine rotationssymmetrische Gleichgewichtsfigur mit f = 1 : 578

Schließlich gelang Alexis Claude Clairaut 1743 die Synthese zwischen der physikalischen und der geodätischen Begründung der ellipsoidischen Erdgestalt. Seine Theorie erlaubt die Berechnung der Abplattung aus zwei Schweremessungen in verschiedenen Breitengraden.

Nachdem sich das Rotatiosellipsoid als Erdmodell durchgesetzt hatte, wurden bis Mitte des 19ten Jahrhunderts zahlreiche Messungen zur Bestimmung der Ellipsoid-Parameter getätigt.

Die wohl bedeutenste Messung erfolgte 1792-1798 im Auftrag der französischen Nationalversammlung. Jean-Baptiste Joseph Delambre und Pierre Méchain führten die Messung im Meridian von Paris durch. Und zwar zwischen den Orten Barcelona und Dünkirchen.

Diese Messung diente als Grundlage bzw. Bezug für die Meterdefinition von 1791. Dabei stellte sich dann heraus, das das Pariser Urmeter um 0,0856 mm zu kurz geraten war.

Durch Kombination mit einer Messung, die 1735-1744 in Peru von Louis Godin, Pierre Bouguer und Charles Marie de La Condamine getätigt worden war, ergab sich eine Abplattung von f = 1 : 334

Erstes allgemein benutztes Ellipsoid war das durch Friedrich Wilhelm Bessel 1841 aus zehn Gradmessungen berechnete, mit den folgenden Parametern:

Mit den vorliegenden Messungen und Modellen konnte dann Friedrich Robert Helmert, einer der bedeudensten Geodäten der Neuzeit, 1880 die Geodäsie als Wissenschaft von der Ausmessung und Abbildung der Erdoberfläche definieren.

Um geodätische Resultate miteinander vergleichen und um anderen Wissenschaften einheitliche Ergebnisse zur Verfügung stellen zu können, mußten Bezugsysteme geschaffen bzw. festgelegt werden. Dies geschieht durch die Internationale Union für Geodäsie und Geopysik, kurz auch IUGG genannt.

Die Generalversammlung von 1924 in Madrid führte das 1909 von John Fillmore Hayford, aus astrogeodätischem Material der USA, berechnete Ellipsoid als Internationales Referenz Ellipsoid (IRE) ein. Es besitzt die Parameter:

Die Genaralversammlung der IUGG, die 1930 in Stockholm stattfand, erweiterte das Hayford-Ellipsoid durch die Internationale Schwereformel:

Mit dieser Gleichung wird das Referenzellipsoid auch zum Niveauellipsoid des Erdschwerefeldes.
Das System von 1924/30 ist damit durch vier Parameter definiert:

Dieses System wurde 1967 durch die Genaralversammlung der IUGG in Luzern abgelöst, durch das Geodätische Referenzsystem 1967 mit folgenden Parametern:

Ergänzt wurde der Ellipsoid noch durch folgende Schwereformel:

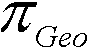
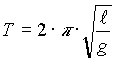
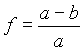
g₀ = 9,780318 ⋅ (1 + 0,0053024 ⋅ sin²(φ) - 0,0000059 ⋅ sin²(2⋅φ)) m/s²

Die Werte des Referenzsystems 1967 stimmen mit den Konstanten der Internationalen Astronomischen Union (IAU) überein, die auf der Generalversammlung von 1964 in Hamburg festgelegt wurden.

Für die Erdrotation gilt dann: ω = 7,292.115.146.7 ⋅ 10^-5 rad/s

Dies ergibt eine Rotationsdauer (Sterntag) von T = 86164,0989 s

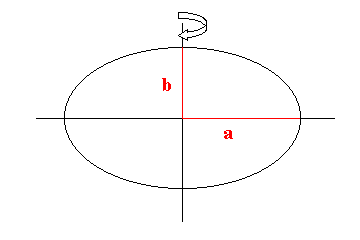
Das Referenzsystem 1967 findet bis heute Anwendung bei wissenschaftlichen Problemstellungen und auch bei neueren Landvermessungen. Es stellt eine optimale Annäherung an das mittlere Erdellipsoid dar, mit Stand 1964.

Ab und zu wird auch das 1961 definierte Geodätische Welt-System benutzt, das diese Parameter besitzt:

Hier noch ein Wert aus dem, in der Enzyklopädia Britannica, veröffentlichten Modell von 1977, mit folgenden Parametern: