Das Kugelmodell der Erde

Betrachtet man die Gestalt der Erde, so kann, in einer allerersten Näherung , eine Kugelgestalt vorausgesetzt werden. Nimmt man jedoch genauere Messungen bezüglich der Erde vor, so ist ein Kugelmodell nicht länger haltbar. Da dieser Sachverhalt Einfluß auf die Länge von Strecken bzw. Größe von Winkeln hat, die auf der Erdoberfläche auftreten, ist es angebracht, sich einmal näher mit der Gestalt der Erde zu befassen.

Schon im Altertum wurde geäußert das die Erde als Kugel behandelt werden kann. Einer der bedeutensten Vertreter dieses Modells war, der als Mathematiker und Philosoph bekannt gewordene, Pythagoras (582 v. Chr.). Im übrigen stammen die Begriffe Mathematik und Philosophie ebenfalls von ihm.

Eine kugelförmige Gestalt der Erde ließ sich aus der Beobachtung von Schiffen schließen, die sich der Küste näherten. Durch die Erdrundung ist die Mastspitze ja zuerst sichtbar. (Dies soll auch Columbus inspiriert haben)

Aristoteles (384-322 v. Chr.). folgerte aus der Beobachtung eines stets kreisförmigen Erdschattens bei Mondfinsternissen auf die Kugelgestalt der Erde.

Ein weiterer Hinweis ergibt sich aus den unterschiedlichen Höhen der Sterne über dem Horizont, wenn an verschiedenen Orten gleichzeitige Messungen vorgenommen werden. (Und der Abstand zwischen den Orten groß genug ist)

Die erste offiziell überlieferte Ermittlung von Umfang und Radius der Erde führte der Alexandriner Eratosthenes (276-195 v. Chr.) durch, der im 3ten Jahrhundert v. Chr. Leiter der Bibliothek in Alexandria gewesen sein soll.
Dies ereichte er durch Winkelmessungen des Sonneneinfalls zur Mittagszeit an zwei verschiedenen Orten, die in etwa auf dem selben Meridian lagen, und zwar Syene(Assuan) und Alexandria.

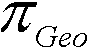
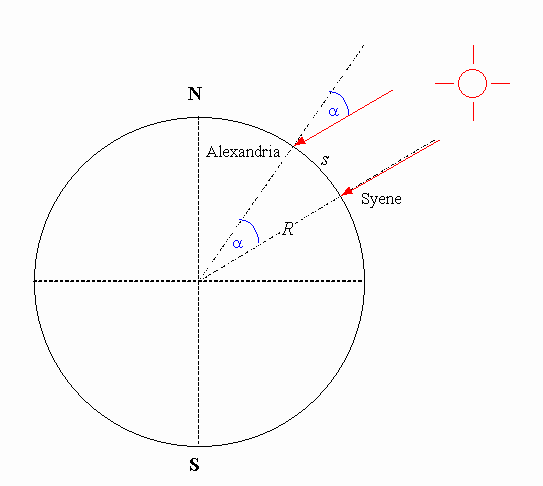
Abbildung 1.1 - Die Winkelmessung des Eratosthenes

Ist nämlich die Entfernung s zwischen den Orten und der Einfallswinkel alpha bekannt, so läßt sich daraus der Erdradius R nach folgender Gleichung ermitteln:

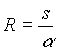
Der von Eratosthenes erhaltene Wert weicht um etwa +16% vom mittleren Radius der Erde ab. Aus heutiger Sicht wurde er damit zum Begründer der wissenschaftlichen Geodäsie.

Es gibt aber auch Autoren, wie z.B. Stecchini oder J. Mitchell, die Zweifel darüber hegen, ob Eratosthenes wirklich der Erste war, der sich eine solche Bestimmung ausdachte. Es sollen Hinweise existieren, das er sein Wissen aus älteren Quellen bezog.

Eine weitere Bestimmung, die überliefert worden ist, stammt von Posidonius (135-51 v. Chr.). Mittels Winkelmessungen, die in den Orten Rhodos und Alexandria getätigt wurden, besitzt sein Wert eine Abweichung von +11% vom mittleren Radius.

Aus dem Kalifat von al-Mamun (827 n. Chr.) ist noch eine Bestimmung des Erdradius bekannt. Aus Winkelmessungen in der Nähe von Bagdad wurde ein Radius ermittelt, der über eine Abweichung von +10% verfügt.

Durch die unselige Verquickung physikalischer Thematiken mit Glaubensfragen kam es in Europa zu einem Stillstand weiterer Erforschung. Erst als das heliozentrische Weltbild anfing sich langsam durchzusetzen, etwa zur Zeit von Kopernikus (1473-1543), bekam die Erdbestimmung neue Impulse.

Mit verfeinerten Methoden bestimmte der französische Arzt Fernel 1525 den Radius der Erde. Durch Winkelmessungen (Breitengradbestimmung durch einen Quadranten) in Paris und Amiens und einer Entfernungsmessung mit einem Rad (Zählung der Umdrehungen) erhielt er einen Wert, der lediglich eine Abweichung von +0,1% besitzt.

Der Niederländer W. Snell van Rojen (lateinisiert Snellius ) der das Brechungsgesetz für Lichtstrahlen auf experimentellem Weg fand (Newton versuchte sein Leben lang vergeblich nach der mathematischen Lösung), konnte durch Anwendung der Triangulation mittels eines keplerschen Fernrohres 1615 durch Messungen zwischen Bergen op Zoom und Alkmaar einen Erdradius bestimmen, der um -3,4% vom mittleren Radius abweicht. Die von Snellius benutzte Methode wurde bis ins 20te Jahrhundert für Gradmessungen und Grundlagennetze verwendet.

Mit einer weiteren Verfeinerung (Fernrohr mit Fadenkreuz) führte der französische Abbe J. Picard 1669/70 zwischen Malvoisine und Amiens eine Gradmessung mittels Triangulation durch. Sein Wert weicht nur um +0,1% vom mittleren Erdradius ab.

Die Messung des Abbe Picard diente Isaac Newton zur Überprüfung seines 1665/66 hergeleiteten Gravitationsgesetzes. Damit war dann insgesamt die mathematische wie auch physikalische Vorraussetzung gegeben, das Kugelmodell der Erde durch ein ellipsoidisches Modell zu verfeinern.

1.0	Kugelmodell als erste Näherung für die Erdgestalt
1.1	Die Vermutung des Pythagoras	582 v. Chr.
1.2	Die Beobachtung und Folgerung des Aristoteles	384-322 v.Chr.
1.3	Die Messung des Eratosthenes	276-195 v.Chr.
1.3	Abb. 1.1 - Die Messung des Eratosthenes
1.4	Die Messung des Posidonius	135-51 v.Chr.
1.5	Die Messung aus dem Kalifat von al-Mamun	827
1.6	Die Messung des Fernel	1525
1.7	Die Messung des Snellius	1615
1.8	Die Messung des Abbe J.Picard	1669/70
1.9	Newtons Ansatz für ein ellipsoidisches Modell	1665/66
1
1

1 - Kugelmodell der Erde

Kugelmodell als erste Näherung der Erdgestalt

Die Vermutung des Pythagoras

Die Beobachtung und Folgerung des Aristoteles

Die Messung des Eratosthenes

Die Messung des Posidonius

Die Messung aus dem Kalifat von al-Mamun

Die Messung des Fernel

Die Messung des Snellius

Die Messung des Abbe J. Picard

Newtons Ansatz für ein ellipsoidisches Modell