Rückrechnungen zum Basisumfang der grossen Pyramide

Wie schon im Kapitel über geodätische Systeme beschrieben, läßt sich der Formfaktor auch noch so darstellen:

Dies erlaubt eine Rückrechnung, um die Grenzen des Numerus der Abplattung n zu bestimmen ! Wir ersetzen in der Gleichung G1 den Formfaktor f_o durch (n-1)/n und stellen dann nach n um.

Setzt man die Werte aus den geodätischen Systemen und den gemessenen Umfang ein, so ergibt sich:

Jahr der Einführung	Geodätisches System	n

1830	Airy	299,3249893
1830	Everest	300,8017264
1841	Bessel	299,1528434
1866	Clarke	294,9786982
1880	Clarke	293,4650061
1909	Hayford (IRE)	296,9999844
1942	Krassowski	298,3000171
1956	Hough	297,0000217
1960	Fischer	298,3000194
1960	WGS	298,2999727
1961	WGS	298,2399887
1966	WGS	298,2500071
1967	IUGG	298,2539163
1967	GRS	298,2471522
1968	Fischer	298,2999687
1969	SüdAm.	298,2500112
1972	WGS	298,2599998
1975	GRS	298,2570257
1976	SAO/GRIM2	298,2550074
1977	Enz. Brit.	297,9999804
1980	GRS	298,2572341
1984	WGS	298,2572341

Tabelle 6.1

Man erhält also folgende maximale Grenzen:	293 < n < 301
Bei Beschränkung auf die modernen Systeme:	297 < n < 299

Mit diesen Grenzen für n läßt sich dann auch eine Rückrechnung für die Pol- bzw. Äquatorachsen tätigen. Wieder von den Gleichungen G1 und G2 ausgehend, ergibt sich durch Einsetzen von n und Umstellung nach a bzw. nach b :

Werden die Werte für n in 0,25er Schritten ausgeführt, ergibt sich für die Achsen folgende Tabelle:

n	2b	2a

297	12.713.696,35	12.756.648,03
297,25	12.713.660,23	12.756.575,53
297,5	12.713.624,16	12.756.503,16
297,75	12.713.588,16	12.756.430,92
298	12.713.552,22	12.756.358,79
298,24	12.713.517,77	12.756.289,66
298,25	12.713.516,34	12.756.286,79
298,255	12.713.515,62	12.756.285,35
298,5	12.713.480,52	12.756.214,90
298,75	12.713.444,75	12.756.143,14
299	12.713.409,05	12.756.071,50

Tabelle 6.2

Aus der Tabelle 6.2 ergeben sich die maximalen Grenzen der Achsen mit:

12.713.409 < 2b < 12.713.697

12.756.071 < 2a < 12.756.649

Noch einmal zum Vergleich die Werte für die Achsengrenzen aus den geodätischen Systemen.

12.712.160 < 2b < 12.713.824

12.754.790 < 2a < 12.756.776

Eingeschränkt auf die modernen Systeme

12.713.540 < 2b < 12.713.554

12.756.310 < 2a < 12.756.360

Verglichen mit den modernen geodätischen Systemen, ergibt sich eine gute Übereinstimmung, da die Intervalle der geodätischen Systeme innerhalb der berechneten Bereiche liegen, und diese Grenzen auch nicht mehr als 100 m voneinander entfernt sind.

Die errechneten Werte für die Achsen in die differenzierte Gleichungen G1 und G2 für den Pyramidenumfang eingesetzt, ergeben dann folgendes Gesamtbild :

n	2b	2a	U_B

297	12.713.696,35	12.756.648,03	921,4530721
297,25	12.713.660,23	12.756.575,53	921,4530724
297,5	12.713.624,16	12.756.503,16	921,4530719
297,75	12.713.588,16	12.756.430,92	921,4530720
298	12.713.552,22	12.756.358,79	921,4530722
298,24	12.713.517,77	12.756.289,66	921,4530720
298,25	12.713.516,34	12.756.286,79	921,4530723
298,255	12.713.515,62	12.756.285,35	921,4530720
298,5	12.713.480,52	12.756.214,90	921,4530723
298,75	12.713.444,75	12.756.143,14	921,4530717
299	12.713.409,05	12.756.071,50	921,4530717

Durch Vergleich läßt sich erkennen, dass für 297,75 < n < 298,5 eine gute Übereinstimmung zwischen Basisumfang der großen Pyramide und den Achsen der Erde, bzw. den modernen geodätischen Systemen besteht.

Die aus dem Umfang der Pyramide abgeleiteten Erdmaße lassen sich ohne weiteres in die Reihe der modernen geodätischen Systeme einfügen.

Der Basisumfang der großen Pyramide bezieht sich also, wie gesehen, auf den kleinen Schmiegekreis. Die Gleichung für den Basisumfang U_B der großen Pyramide von Gizeh, in Abhängigkeit vom Radius r₁ des kleinen Schmiegekreises lautet also:

Setzt man die Werte aus den modernen geodätischen Systemen für r₁ in die Gleichung G3 ein so lassen sich dadurch folgende Grenzen ermitteln:

U_B : 921,45385 m ± 0,00185 m

921,4520 m < U_B-GeoSys < 921,4557 m

Zum Vergleich noch mal die Werte aus dem Fehleransatz:

U_B : 921,45307 m ± 0,006 m

921,447 m < U_B < 921,459 m

Der Basisumfang nach dem Fehleransatz läßt sich mit einer Abweichung von höchstens 1 mm aus den Daten der modernen geodätischen Systeme ableiten.

Ersetzt man in der Gleichung G1 den Formfaktor f_o durch (n-1)/n und stellen dann nach n um, erlaubt dies eine Rückrechnung für n, den Numerus der Abplattung.

Man erhält so folgende maximale Grenzen:

296 < n < 309

Bei Beschränkung auf die modernen Systeme:

297 < n < 299

Mit diesen Grenzen für n ließ sich eine Rückrechnung für die Pol- bzw. Äquatorachsen tätigen.

Von den Gleichungen G1 und G2 ausgehend, ergab sich durch Ersetzen des Formfaktor f_o durch (n-1)/n und Umstellung nach a bzw. nach b :

Die Werte für n wurden in 0,25er Schritten ausgeführt, und für die Achsen ergab sich eine Tabelle, aus der sich die maximalen Grenzen der Achsen ergaben:

12.713.409 < 2b < 12.713.697

12.756.071 < 2a < 12.756.649

Noch einmal zum Vergleich die Werte für die Achsengrenzen aus den geodätischen Systemen.

12.712.160 < 2b < 12.713.824

12.754.790 < 2a < 12.756.776

Eingeschränkt auf die modernen Systeme

12.713.540 < 2b < 12.713.554

12.756.310 < 2a < 12.756.360

Die aus dem Umfang der Pyramide abgeleiteten Erdmaße lassen sich ohne weiteres in die Reihe der modernen geodätischen Systeme einfügen.

Die errechneten Werte für die Achsen. mit dem zugehörigen Numerus, in die Gleichungen G1 und G2 für den Pyramidenumfang eingesetzt, ergaben dann die Tabelle 6.3

Durch Vergleich ließ sich erkennen, dass für 297,75 < n < 298,5 eine gute Übereinstimmung zwischen Basisumfang der großen Pyramide und den Achsen der Erde, bzw. den modernen geodätischen Systemen besteht.

n	2b	2a	U_B

297,75	12.713.588,16	12.756.430,92	921,4530720
298	12.713.552,22	12.756.358,79	921,4530722
298,24	12.713.517,77	12.756.289,66	921,4530720
298,25	12.713.516,34	12.756.286,79	921,4530723
298,255	12.713.515,62	12.756.285,35	921,4530720
298,5	12.713.480,52	12.756.214,90	921,4530723

Tabelle 6.4

Durch die Teilung in 0,25er Schritten ist es also möglich, ein Fenster herauszufiltern, in dem Korrelation zwischen den Erdmaßen und dem Basisumfang der großen Pyramide von Gizeh besteht.

Trägt man die biher ermittelten Intervalle für den Basisumfang der großen Pyramide graphisch über dem Basisumfang auf, so ergibt sich die in Abbildung 6.1 dargestellte Situation. Die Auflösung beträgt 1 Teilstrich = 0,01 m

Abbildung 6.1 - Vergleich für den Basisumfang der großen Pyramide

Verfeinert man die Auflösung ergibt sich folgendes Bild. Die Auflösung beträgt 1 Teilstrich = 0,005 m

Abbildung 6.2 - Verfeinerter Vergleich für den Basisumfang der großen Pyramide

Durch die untere Grenze der Messung von Stadelmann und der oberen Grenze des Fehleransatzes wird ein Fenster aufgespannt, in dem sich fast alle Ansätze befinden. Die folgende Abbildung zeigt die Situation. Die Auflösung beträgt 1 Teilstrich = 0,01 m

Abbildung 6.3 - Fenster für den Basisumfang der großen Pyramide

Verfeinert man die Auflösung ergibt sich folgendes Bild. Die Auflösung beträgt 1 Teilstrich = 0,005 m

Abbildung 6.4 - Verfeinertes Fenster für den Basisumfang der großen Pyramide

Das Fenster erstreckt sich dann von 921,437 m bis 921,45907 m. Das entspricht einer Intervallbreite von 2,27 cm.

Der Mittelwert beträgt 921,448035 m ± 0,011 m

Alle Ansätze die auf physikalischen oder geophysikalischen Größen beruhen befinden sich innerhalb des Fensters.

Das maximale Fenster für den Basisumfang ergibt sich aus den Grenzen durch die geodätischen Systeme Nur in diesen Grenzen ist eine Relation zwischen Erddaten und Basisumfang möglich. Die nächste Abbildung zeigt diese Situation. Die Auflösung beträgt 1 Teilstrich = 0,01 m

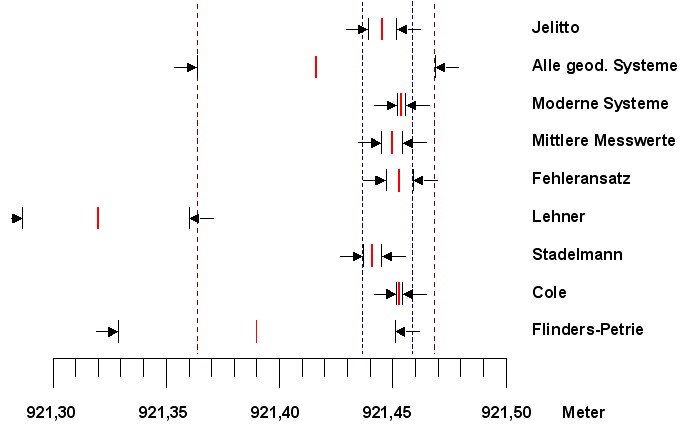
Abbildung 6.5 - Maximales Fenster für den Basisumfang der großen Pyramide

Das maximale Fenster erstreckt sich dann von 921,3639 m bis 921,4687 m. Das entspricht einer Intervallbreite von 10,48 cm.

Der Mittelwert beträgt 921,4163 m ± 0,0524 m

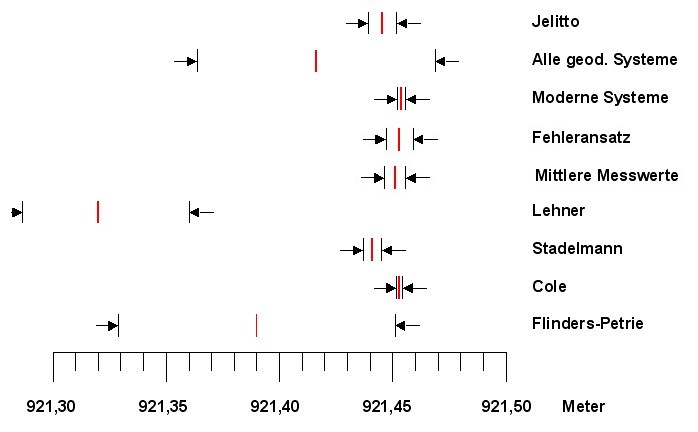
Wäre der Basisumfang der großen Pyramide von Gizeh nur 15 cm grösser oder kleiner, hätte man schon zweifelsfrei zeigen können, dass zwischen Basisumfang und den geodätischen Systemen keine Relation besteht. Es war aber zu sehen, dass der Basisumfang genau in ein Fenster von 2,27 cm fällt, das durch alle relevanten Messwerte sowie Ansätze und deren Toleranzen aufgespannt wird.

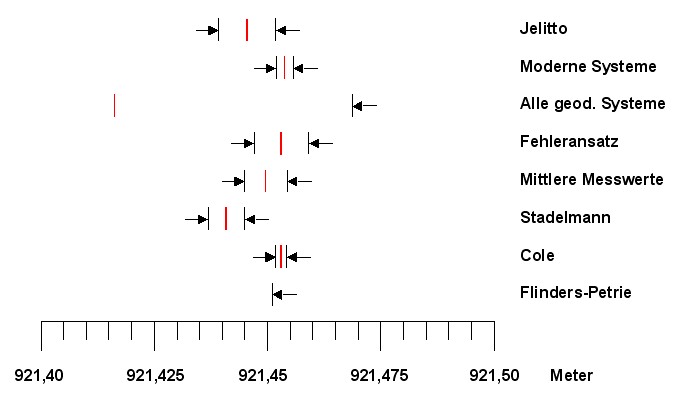
Das minimalste Fenster wird durch die Grenzen der modernen gedätischen Systeme gebildet. Das nächste Bild zeigt die Stituation:
Hier ist noch einmal deutlich zu erkennen, dass die gemessenen Basisumfänge gut in die Intervalle aus den geodätischen Systemen passen. Und auch, dass das Intervall durch die modernen Systeme fast identisch mit der Messung von Cole ist. Die Auflösung beträgt 1 Teilstrich = 0,005 m

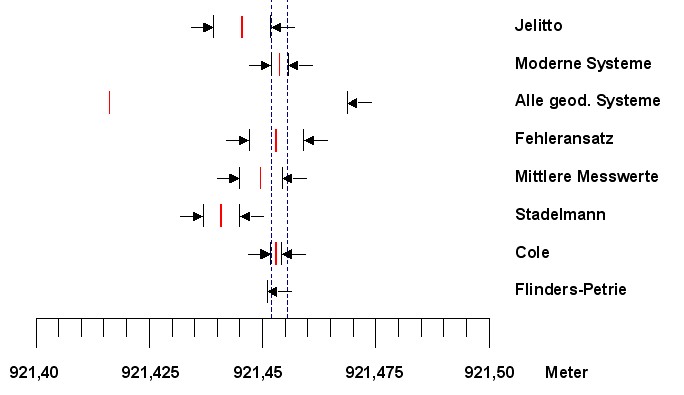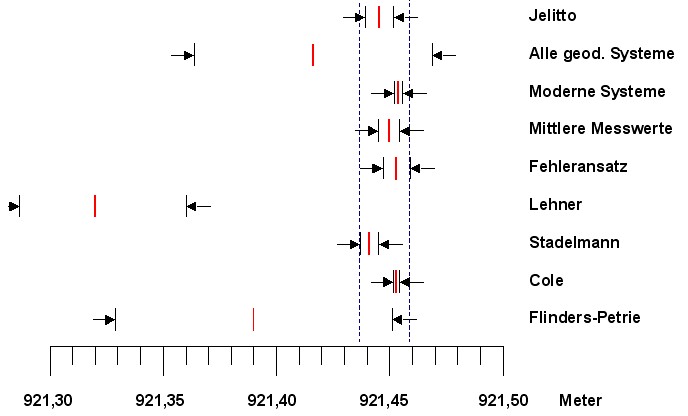
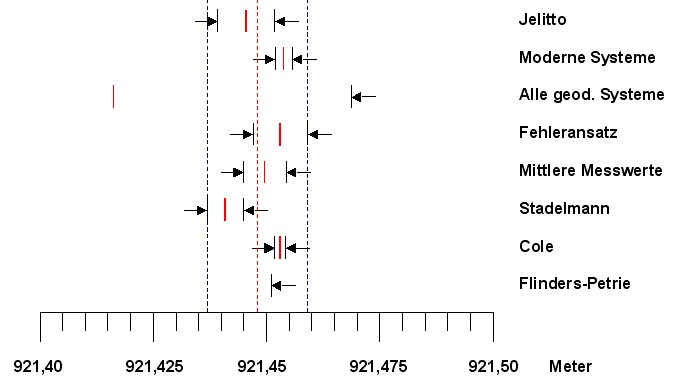
Abbildung 6.6 - Minimales Fenster für den Basisumfang der großen Pyramide

Es ist zu sehen, dass der Basisumfang nach Cole (und dem Fehleransatz) genau in das Fenster fällt, das durch die geodätischen Systeme und deren Toleranzen aufgespannt wird.

Damit hat sich hinreichend gezeigt, dass zwischen dem Basisumfang (Cole) der großen Pyramide von Gizeh und den Erddaten eine Relation besteht.

Aus den bisherigen Betrachtungen läßt sich sogar noch eine andere Konsequenz ziehen. Da praktisch nur die modernen Systeme ab 1961 eine hinreichende Genauigkeit liefern, wäre es vor diesem Zeitpunkt zwar möglich gewesen, exakte Beziehungen zwischen Erddaten und der sogenannten Cheops-Pyramide herzuleiten, aber beweisbar wäre es nicht gewesen.
Heißt also, vor 1961 wäre schon eine ziemlich große Portion Glück von nöten gewesen, um dass hier abgeleitete Verhältnis zu erhalten. Zumal es ja, aufgrund der mangelnden Genauigkeit, keine Möglich keit gegeben hat, die Richtigkeit dieses Verhältnisses zu belegen oder auch zu widerlegen.
An dem nahe 1 liegenden Proportionalitätsfaktor aus dem Ansatz läßt sich aber sehen, dass wegen der fehlenden Genauigkeit, bis jetzt alle lassischen Interpretatoren eine quantitative Lösung verfehlt haben.
Daraus ergibt sich dann auch die Konsequenz, dass die gesamte klassische Diskussion (Piazzi Smith u.a.) um die Maße der Pyramide, sich auf rein spekulativen Boden bewegt hat.

Abschließend noch ein paar Worte zu einem häufig vorgebrachten Argument. Man könnte das hier erzielte Ergebnis als zufällige Übereinstimmung ansehen. Wenn es das einzige Ergebnis wäre, bei dem eine solche Übereinstimmung auftritt, wäre das auch in Betracht zu ziehen.
Hier sei noch ein mal erwähnt, dass die gesamte globale Lage des Gizeh-Komplexes sich ebenfalls aus der Schmiegekreis-Konstruktion bzw. den Erddaten ableiten läßt. Und das mit einer ähnlichen Genauigkeit wie beim Basisumfang.
Letzten Endes treten am Gizeh-Komplex derart viele Übereinstimmungen mit geometrischen bzw. geodätischen Daten auf, dass es dann etwas merkwürdig erscheint die gesamte Konstruktion durch das Auftreten von 7 bis 8 Zufällen zu erklären.

Man kann eher davon ausgehen das hinter dem Gizeh-Komplex ein wohl durchdachter Gesamtpaln gestanden hat.

Seite: 0 1 2 3 4 5 6 7 a 8 a 9 a 10 a 11 a 12 a 13 a 14

6 - Rückrechnungen zum Basisumfang der grossen Pyramide

6.1 - Rückrechnung für den Numerus der Abplattung

6.2 - Rückrechnung für die Achsen

6.3 - Ableitung des Basisumfanges aus den Werten der geodätischen Systeme

6.4 - Ableitung der geodätischen Werte aus dem Basisumfang

6.5 - Das Fenster bezüglich der geodätischen Werte und dem Basisumfang

6.6 - Konsequenzen