Copyright © Klaus Piontzik
 |
Die, in diesem Buch, entwickelte
Betrachtungsweise geht vom Gesamtfeld also der
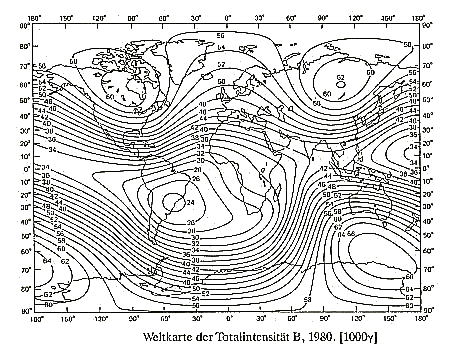
Totalintensität der Erde aus. Alle folgenden Betrachtungen und Analysen beruhen daher auf den realen, letztlich gemessenen, Werten des magnetischen Feldes. Hier eine Abbildung des Gesamtfeldes von 1980, wie es von diversen geophysikalischen Instituten als „International Geomagnetic Reference Field“ kurz IGRF herausgegeben wird. Eine Tabelle der Werte findet man hier: Tabelle des Erdmagnetfeldes |
|
| Abbildung 2.1 - Das magnetische Gesamtfeld der Erde - IGRF 1980 |
| Auffallend sind hier die vier Extremwerte des Feldes (und nicht nur zwei wie beim Stabmagneten- bzw. Dipolmodell), wobei drei Maxima und ein Minima vorliegen. Hinzu kommt noch ein Sattelpunkt (etwa Indonesien). |
| Hier muss darauf hingewiesen werden, dass inzwischen
zwei Modelle des Erdmagnetfeldes existieren, das IGRF
und das WMM.
|
IGRF |
|
Zum einen gibt es das International
Geomagnetic Reference Field kurz IGRF.
Verantwortlich für das IGRF ist die „International
Association of Geomagnetism and Aeronomy“ (IAGA),
einer der sieben Abteilungen der IUGG (International
Union of Geodesy and Geophysics). Das IGRF wird durch die IAGA Working Group V-8 angefertigt, die für “Analysis of the Global and Regional Geomagnetic Field and Its Secular Variation” zuständig ist. Das 10te Modell basiert auf einer Revision von Juli 1995 (XXI General Assembly of the International Union of Geodesy and Geophysics in Boulder, Colo.) durch die IGRF unter Hinzunahme benachbarter Modelle, die durch das NASA's „Goddard Space Flight Center“, dem „Institute of Terrestrial Magnetism, Ionospheric and Radio Wave Propagation“ IZMIRAN sowie der U.S. Navy und dem „British Geological Survey“ bereit gestellt wurden. Das Modell wird für jeweils 5 Jahre angefertigt und ist mittlerweile auch über das Internet verfügbar. Das zur Zeit gültige Modell ist das IGRF11 |
 |
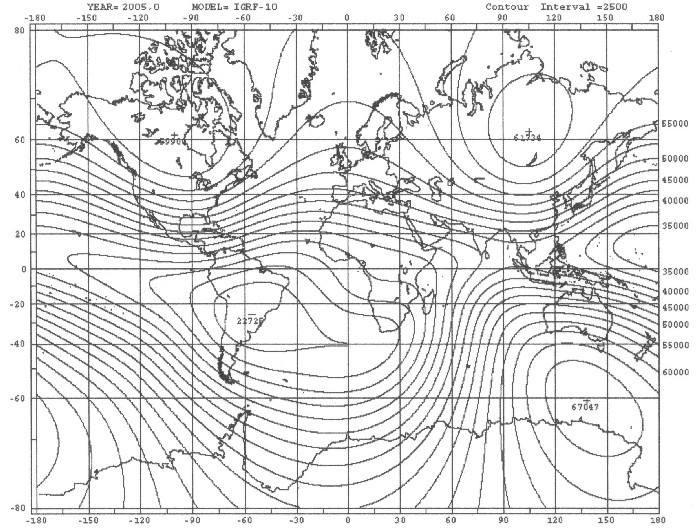| Abbildung 2.2 - Das magnetische Gesamtfeld der Erde – IGRF - 2005 |
WMM |
|
Zum anderen kann man das WMM 2005 über das
„National Geophysical Data Center“ (NGDC)
beziehen, mittlerweile ebenso über das Internet. Das
“World Magnetic Model” (WMM)
ist ein Erzeugnis der U.S. National
Geospatial-Intelligence Agency (NGA). Das NGDC und das British Geological Survey (BGS) fertigten das WMM mit Unterstützung der NGA in den USA an, zusammen mit der „Defence Geographic Imagery“ sowie der „Intelligence Agency“ (DGIA) aus Großbritannien. Das WMM wird als Standardmodell benutzt, für das US Department of Defense, das UK Ministry of Defence, der North Atlantic Treaty Organization (NATO), und dem World Hydrographic Office (WHO). Es ist inzwischen auch in der zivilen Navigation weit verbreitet. Das Modell, die zugehörige Software und Dokumentation werden von der NGDC und der NGA verwaltet. Das Modell wird für jeweils 5 Jahre angefertigt. Das zur Zeit gültige Modell ist das WMM2010 |
 |
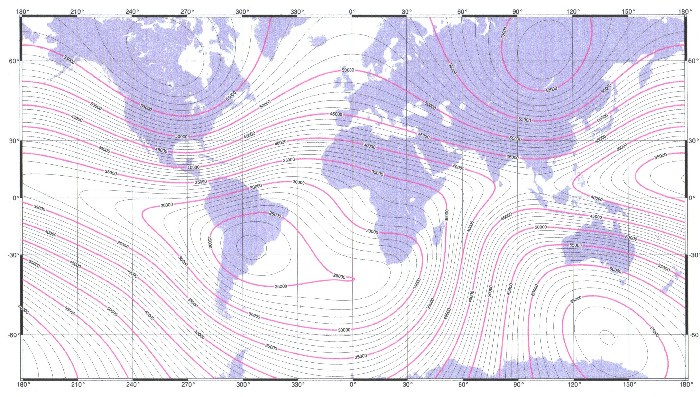| Abbildung 2.3 - Das magnetische Gesamtfeld der Erde – WMM - 2005 |
| Das WMM 2005, ist z.B. unter dem Titel „The US/UK World Magnetic Model for 2005-2010“ als NOAA Technical Report NESDIS/NGDC-1 von McLean, Macmillan, Maus, Lesur, Thomson und Dater seit Dezember 2004 im Internet erhältlich. Es enthält das Modell mit seinen mathematischen Ableitungen und auch alle relevanten Karten, wie Deklination, Inklination, Vertikalintensität usw. zum Erdmagnetfeld. |
| Im Buch wird gezeigt
dass sich die Gesamtfeldstruktur in den letzten 300
Jahren nicht wesentlich geändert hat und das Feld der Totalintensität temporär, über längere Zeiträume, also quasi konstant ist und sich daher für eine allgemeine Analyse des Erdfeldes bestens geeignet |
| Die (Fourier)Analyse des Erdfeldes wird ausführlich erst im Kapitel 8 geschehen |
| Die Koordinaten der eigentlichen Extremwerte lassen sich auf zwei Arten bestimmen. Einerseits, indem man die Ränder der extremalen Gebiete aus Abb. 2.1 ermittelt und daraus die Mittelwerte bildet: |
Die Koordinaten für die Extremwerte 1
| Name | Breite |
Länge |
| Nord-Maximum | +56,8875 Grad Nord | - 96,125 Grad West |
| Süd-Maximum | -61,975 Grad Süd | +144,95 Grad Ost |
| Grosse Anomalie | +59,5375 Grad Nord | +107,125 Grad Ost |
| Minimum | -26,05 Grad Süd | - 50,8375 Grad West |
| Sattelpunkt | +6,5 Grad Nord | +99,3125 Grad Ost |
Die Namen der Extrema stammen aus der Geophysik und sind dort üblich.
 |
Eine zweite Möglichkeit der Auswertung
besteht darin, die Totalintensitäten der Abbildung 2.1
in eine (numerische Tabelle )
zu übertragen und diese
Werte für eine Analyse zu nutzen. Diese numerische Handhabung erlaubt dann auch eine dreidimensionale Darstellung des Erdfeldes. In der Zeichnung 2.2 sind die drei Maxima und das Minimum noch einmal deutlich zu erkennen. |
|
| Abbildung 2.2 - Die Intensität des magnetischen Gesamtfeldes der Erde in 3D-Sicht | ||
| Aus der angelegten Tabelle lassen sich die Koordinaten der Extremwerte bestimmen: |
Name |
Breite |
Länge |
| Nord-Maximum | +56,344 Grad Nord | - 96,04 Grad West |
| Süd-Maximum | -63,75 Grad Süd | +144 Grad Ost |
| Grosse Anomalie | +60 Grad Nord | +106,5 Grad Ost |
| Minimum | -26,25 Grad Süd | - 50,8145 Grad West |
| Sattelpunkt | +7 Grad Nord | +99 Grad Ost |
| Fasst man beide Ergebnisse zusammen ergeben sich die Bereiche, in denen die magnetischen Extremwerte des Gesamtfeldes liegen. |
Name |
Breite |
Länge |
| Nord-Maximum | 56,344-56,8875 Grad Nord | 96,04-96,125 Grad West |
| Süd-Maximum | 61,975-63,75 Grad Süd | 144-144,95 Grad Ost |
| Grosse Anomalie | 59,5375-60 Grad Nord | 106,5-107,125 Grad Ost |
| Minimum | 26,05-26,25 Grad Süd | 50,8145-50,8375 Grad West |
| Sattelpunkt | 6,5-7 Grad Nord | 99-99,3125 Grad Ost |
| Somit ergeben sich vier Extremwerte des Feldes, wobei drei Maxima und ein Minimum vorliegen. Hinzu kommt noch ein Sattelpunkt. Diese Koordinaten für die Extremwerte und -bereiche werden, in den noch folgenden Untersuchungen, weiterhin genutzt und ausgewertet. |
| Im Jahr 1838 ermittelte Carl Friedrich Gauß folgende Potentialgleichung für das Erdmagnetfeld: |
 |
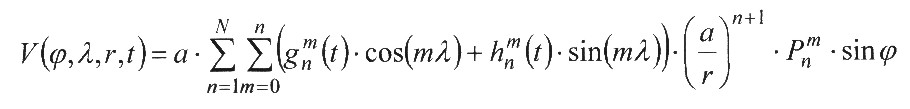| Die magnetische Flussdichte B lässt sich dann mittels des Gradienten aus dem skalaren Potentialfeld ableiten: |
 |
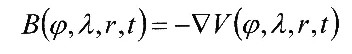(siehe dazu auch „Allgemeine Theorie des Erdmagnetismus“ von C.F. Gauß und W. Weber) |
| Löst man die Klammern auf, so treten in der Gleichung von Gauß lediglich Produkte von Sinus- bzw. Kosinus-Funktionen, sogenannte Kugelflächenfunktionen,auf mit denen wir uns im Kapitel 5 noch beschäftigen werden. |
| Das Magnetfeld der Erde wird weltweit durch mehr als 200 Messstationen erfasst. |
 |
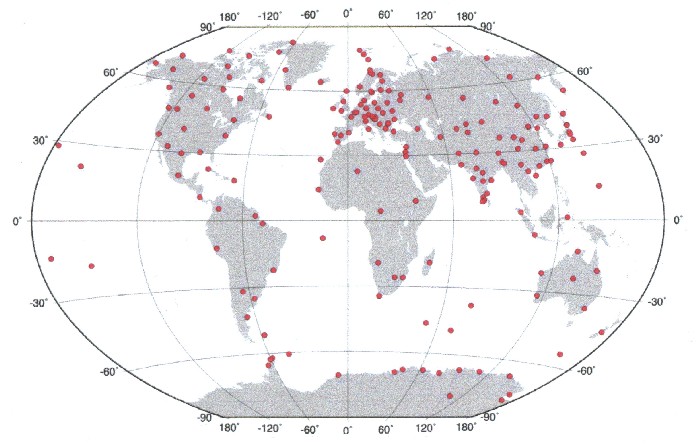| Abbildung 2.8 - Messstationen die mit dem WMM-Modell assoziiert sind |
| Seit einigen Jahrzehnten wird das Feld auch von
Satelliten aus vermessen. Der erste Satellit war Magsat,
der 1980 sechs Monate lang die Intensität und das
gesamte Magnetfeld registrierte. Seit 1999 befindet sich
der dänische Satellit Ørstedt auf einer Erdumlaufbahn
und seit Juli 2000 arbeitet der deutsche Satellit Champ.
Alle anfallenden Daten über das Erdmagnetfeld werden von der IUGG bzw. der IAGA erfasst und ausgewertet. Diese Werte dienen unter anderen als Grundlage zur Erstellung der Modelle IGRF und WMM. Die Karten und damit das Gesamtfeld werden prinzipiell mittels der Gleichung von Gauß berechnet. Dabei geht man aber hin und passt die Koeffizienten gn und hn dem Multipolmodell an !! Diese Handhabung der Gleichung von Gauß ist insofern problematisch, da die Dipoltheorie ja immer noch ein Teil der Betrachtung und Handhabung ist. Ein Ansatz, der auf das Dipolmodell verzichtet, besteht darin, die Totalintensitäten der Abbildung 2.1 bzw. der zugehörigen Tabelle zu nehmen und diese Werte für eine Analyse zu nutzen. Eine vollständige Auswertung des Erdfeldes lässt sich durch eine zweidimensionale Fourieranalyse der Totalintensitäten bewerkstelligen, die in Kapitel 8 noch erfolgen wird. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
