Copyright © Klaus Piontzik
| Der deutsche Physiker Dr. W.O.
Schumann von der Technischen Universität
München wollte seinen Studenten 1952 Übungsaufgaben zur
Elektrizitätslehre stellen. Thema war damals die
Berechnung von Hohlraumresonatoren.
Dabei gab er vor, dass die Unterseite der Ionosphäre,
also die Heavisideschicht, die eine Kugel und die
Erdoberfläche die andere Kugel des Resonators sein
sollte. Die Aufgabe bestand darin, die Eigenfrequenz
(Resonanz) dieses Hohlraumresonators zu ermitteln. Als
Ergebnis erhielt er f = 7,8 Hz.
Es sei darauf hingewiesen das sich die Aufgabe nur mittels der Differential bzw. Integralrechnung lösen lässt. Und die Lösung erfolgt über die Ermittlung sogenannter transversalmagnetischer Wellen (TM-Wellen) in einem Hohlraumresonator. Diese werden heute als Schumannwellen oder auch Schumann-Resonanzen bezeichnet. (siehe dazu Zeitschrift Naturforschung 7a, S. 149-154, 1954, von W.O. Schumann und auch Zeits. Angew. J. Phys. 9, 373–378, 1957) Die Schumann-Frequenz wird manchmal als die Resonanzfrequenz der Erde bezeichnet. Wie im vorherigen Kapitel 6 zu sehen war, liegt die erste Eigenfrequenz der Erde (also der Oberfläche) etwas höher bei 11,75 Hz bzw. 11,79 Hz. |
Die
Schumann-Frequenz ist lediglich die Eigenfrequenz |
| Ein Hohlraum-Resonator braucht eine Anregung um
selber ins Schwingen zu geraten. Dies erfolgt, im Fall
des Schumann-Resonators, durch den Sonnenwind und durch
Gewitter (weltweit täglich etwa 3000). Durch
Schwankungen der anregenden Einflüsse ist die
resultierende Schwingung aber ebensolchen Schwankungen
unterworfen, sowohl in der Intensität wie in der
Frequenz. Einen Hinweis liefern hier die Messungen, die in den letzten Jahren bzgl. der Schumann-Frequenz gemacht worden sind und die zu unterschiedlichsten Resultaten führten. Wie noch in Kapitel 14 zu sehen sein wird, stellt die Ionosphäre eine Schwingungsschicht dar. Und daher geht der momentane Schwingungszustand (der Ionosphäre) in die Messung mit ein. Zumal hier auch langfristige Veränderungen möglich sind. Durch die Messanordnung bedingt kann man also verschiedene Werte für die Schumann-Frequenz erhalten. Die Erdfrequenz ist dagegen als eine Konstante anzusehen. Die Frage ist nun, ob sich ein Zusammenhang zwischen der Schumann-Frequenz und den Erdfrequenzen herstellen lässt. Hier ist die Antwort: |
Die Äquatorfrequenz (11,75 Hz) mal 2/3 ergibt die Schumann-Frequenz.Das heisst, Äquator- und Schumannfrequenz stehen im Verhältnis einer Quinte zueinander. |
 |
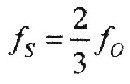| Die Ableitung dieser Beziehung geschieht aber erst in
Kapitel 15, da in den dazwischen liegenden Kapiteln
(hauptsächlich Kapitel 11 und Kapitel 12) noch Betrachtungen
angestellt werden, die eine direkte Ableitung erst
möglich machen.
Trägt man die ersten Grundfrequenzen der Erde (rote Linien) in das Spektrum der Schumannfrequenzen (von der Stanford University, California) ein, so ergibt sich das folgende Bild 7.1: |
 |
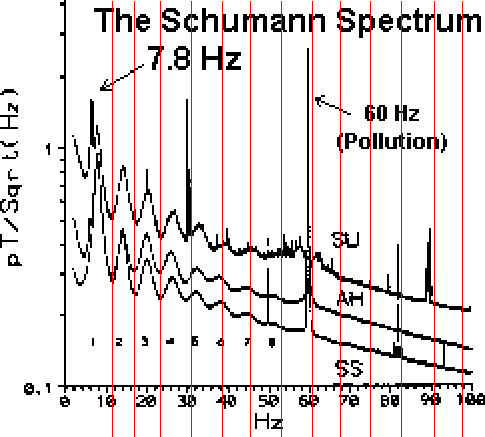| Abbildung 7.1 - Grundfrequenzen und Schumann-Spektrum |
| Die Grundfrequenzen liegen bei den niedrigen
Frequenzen(<30Hz) quasi in einer gegenphasigen
Anordnung zum Schumann Spektrum. Bei höheren Frequenzen
(>50Hz) gleichen sich die beiden Spektren an. Das
Schumann-Spektrum steht also in Korrelation zum
Spektrum der Erdfrequenzen. In Kapitel 15 erfolgt eine
detaillierte Betrachtung dieses Zusammenhanges.
Die von W. O. Schumann ermittelte Frequenz wird heute als „biologisches Normal“ bezeichnet, da sich durch Messungen an freiwilligen Versuchspersonen gezeigt hat, dass der Mensch diese Signale braucht. Dies wurde bis heute durch mehrere unabhängige Wissenschaftler bestätigt. Einer davon ist Michael A. Persinger der im Auftrag der NASA handelte. Während der ersten bemannten Raumflüge stellten sich erhebliche physiologische Probleme bei den Astronauten ein, und dies konnte nur durch die Installation von Schumannwellen - Generatoren behoben werden. (siehe dazu in “The effect of pulsating magnetic fields upon the behavior and gross physiological changes of the albino rat Undergraduate thesis” von Persinger, M. A). Ein anderer Wissenschaftler ist Rüdger Wever am Max Planck-Institut in Erling - Andechs. Er führte Experimente mit Freiwilligen durch, die einen Monat lang in einem magnetisch abgeschirmten Bunker beobachtet wurden. Dabei traten Störungen bei den sogenannten circadianen Rhythmen (innere Uhren) auf. D.h. es kam zur Destabilisierung des Wach-Schlaf-Rhythmus, des Tagesganges der Körpertemperatur und des Cortison-Spiegels im Blut, um nur einige Beispiele zu nennen. (siehe dazu „Einfluß schwacher elektromagnetischer Felder auf die circadiane Periodik des Menschen“ und „The effects of electric fields on circadian rhythmicity“ in „men. Life Sci. Space Res. 8“ von Rütger Wever) Bemerkenswert in diesem Zusammenhang ist die Arbeit von O’Keefe und L. Nadel, die nachweisen konnten das die Frequenz von 7,8 Hz im Hippocampus, vorkommt. Dieses Hirnareal ist für Aufmerksamkeit und Konzentration wichtig, und ist praktisch bei allen Säugern vorhanden. (vergleiche mit „Informative Medizin“ von Wolfgang Ludwig – Kapitel 7). |
Siehe dazu auch: Planetare Systeme - Schumann Frequenz
Siehe dazu auch: Planetare Systeme - Erhöhung der Schumann Frequenz
|
Zwischen 1978 und 1979 fanden in
Pfaffenhofen/Ilm durch Hans Baumer
spezielle Frequenzmessungen statt. Mit einer
schmalbandigen Bandbreite (2 kHz) wurden die
Frequenzbereiche um 10 kHz und 27 kHz fortlaufend über
eine Empfangsanlage aufgenommen. Die Reichweite des
Empfängers wurde dabei auf 400-500 Km beschränkt. Dies
führte zur Entdeckung der Sferics, die
auch als Wetterfrequenzen bekannt sind.
Die Grundfrequenz der Sferics wird dabei mit 4150,84
Hertz angegeben. (siehe dazu in“ Das natürliche elektromagnetische Impuls-Spektrum der Atmosphäre“ 1982 von Baumer und Eichmeier sowie in „Sferics“ Seite 285, 1987 von Hans Baumer) Legt man die in Kapitel 6 ermittelten Erdfrequenzen zugrunde, so ergibt sich die folgende Primfaktorenzerlegung. Bestimmt man die 11te Eigenschwingung der Grundfrequenz und betrachtet die entsprechenden Oktaven, so zeigt sich für die 5te Oktave: |
| für den Polradius : 4150,19 Hz =
11,79*11*25 für den Äquatorradius : 4136,27 Hz =11,75*11*25 |
|
Die Sferic-Grundfrequenz ist die 5. Oktave der 10. Oberwelle der Erdgrundfrequenz (auf den Polradius bezogen) Bemerkung: 11. Eigenschwingung = 10. Oberwelle Vergleicht man die gemessene Sfericfrequenz mit den beiden abgeleiteten Frequenzen ist die Konsequenz also, dass die Sfericfrequenz in Relation zum Polradius steht und nicht zum Äquatorradius. Der Unterschied zwischen Polfrequenz und Äquatorfrequenz beträgt immerhin etwa 14 Hertz. In seinem Buch „Die kosmische Oktave“ (Seiten 38-41) stellt Cousto einen Zusammenhang zwischen Sfericfrequenz und Sterntag her. Der Vergleich mit der Erdrotation liefert eine Differenz von etwa 3 Hz. Um den Zusammenhang zwischen Sferics und Sterntag aufrecht zu erhalten, muss er die Sfericfrequenzen herunter teilen (Seite 199) und kann sie dann erst mit der siderischen Tonleiter vergleichen. Durch diese Teilung wird auch der Fehler entsprechend verkleinert. Stellt man von vornherein den Bezug zum Polradius her, ist dieser „Rechentrick“ nicht nötig. Es ist auch manchmal nachzulesen, dass die Differenz als Messfehler interpretiert wird. Hier sollte man sich folgendes vor Augen halten: Der gemessene Wert für die Sfericgrundfrequenz wird mit 2 Stellen hinter dem Komma angegeben. Damit beläuft sich der Fehler aber höchstens auf ±0,05 Hz oder mit einer gewissen Großzügigkeit auf ± 0,1 Hz. Richtet man sich nach Cousto`s Angabe und interpretiert den Messwert mit einem Fehler von 14 Hz, so wäre die ganze Messung zwecklos, da sie mit einem systematischen Fehler behaftet wäre. Heutige Messungen, gerade im elektrotechnischen Bereich (also auch bei Frequenzen), sind jedoch sehr exakt, so dass die Angabe von 4150,84 Hz als korrekt anzusehen ist. Wie der Schwingungsansatz auch zeigt, lässt sich die Sfericgrundfrequenz mit hinreichender Genauigkeit (Ungenauigkeit < 0,7 Hz) ableiten. |
Die Sfericfrequenzen stehen in Abhängigkeit zum Poldurchmesser der Erde |
| Oder auch allgemeiner ausgedrückt: |
Die Sfericfrequenzen stehen in Relation zur Erdfrequenz |
| Eine umfassende Betrachtung der Sferics erfolgt in Kapitel 15.6 |
Siehe dazu auch: Planetare Systeme - Sferics
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
