Copyright © Klaus Piontzik
| Durch die Interferenz
verschiedener Wellen entstehen also Schwingungsmaxima und
Minima bzw. Schwingungsschichten, die die Erde kugelförmig
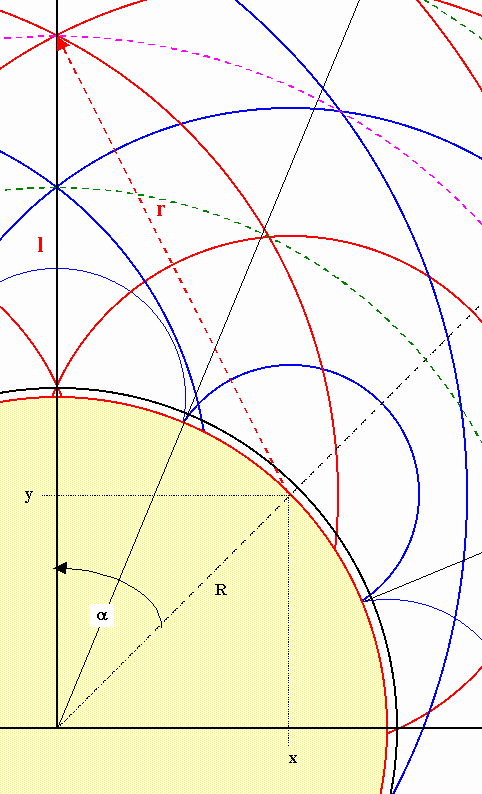
einhüllen. Siehe dazu auch Kapitel 5.6 und 5.7 In der folgenden Abbildung 12.1 wird ein geometrischer Ansatz zur Berechnung der Distanz einer Schicht vom Erdmittelpunkt benutzt: |
 |
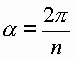
|
|||
| Vielfache des Grundwinkels: | ||||
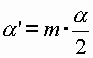 |
m<n | |||
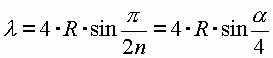 |
||||
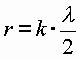 |
||||
| R=6355758,426 m | ||||
| Abbildung 12.1 - Distanzberechnung der Interferenzenschichten | ||||
| Einsetzen aller obigen Terme in die Gleichung für l' führt zu folgendem Ergebnis: |
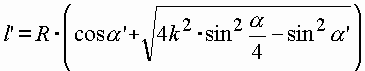 |
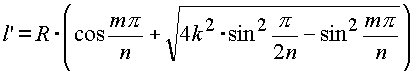 |
| Das Buch enthält eine detallierte Ableitung der Schichtungen |
| Systematisches Einsetzen der Parameter n, m und k in die Gleichung führt zu einer Tabelle, in der dann die Mittelpunktabstände aller berechneten magnetischen Schichten enthalten sind. |
| Tabelle der Distanzen der Extremal-Schichten für n < 6 | ||||||||||
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| n | m | |||||||||
| 1 | 1 | 6355,76 | 19067,28 | 31778,79 | 44490,31 | 57201,83 | 69913,34 | 82624,86 | 95336,38 | Km |
| 2 | 1 | 6355,76 | 16815,76 | 26205,46 | 35387,37 | 44490,31 | 53554,57 | 62596,96 | 71625,76 | Km |
| 2 | 2 | 2632,64 | 11621,04 | 20609,44 | 29597,84 | 38586,24 | 47574,64 | 56563,04 | 65551,44 | Km |
| 2 | 4 | 15344,16 | 24332,56 | 33320,96 | 42309,36 | 51297,76 | 60286,16 | 69274,56 | 78262,96 | Km |
| 3 | 1 | 6355,76 | 14635,89 | 21433,41 | 27997,91 | 34476,36 | 40913,10 | 47326,39 | 53725,14 | Km |
| 4 | 1 | 6355,76 | 13122,94 | 18378,41 | 23426,02 | 28397,82 | 33333,04 | 38247,73 | 43149,72 | Km |
| 4 | 2 | 7365,95 | 13136,72 | 18390,65 | 23477,33 | 28486,50 | 33452,99 | 38393,37 | Km | |
| 4 | 3 | 4134,54 | 9390,01 | 14437,62 | 19409,42 | 24344,64 | 29259,33 | 34161,32 | Km | |
| 4 | 4 | 3373,22 | 8237,70 | 13102,19 | 17966,68 | 22831,16 | 27695,65 | 32560,14 | Km | |
| 5 | 1 | 6355,76 | 12052,97 | 16318,30 | 20403,63 | 24423,72 | 28412,40 | 32383,47 | 36343,66 | Km |
| 5 | 2 | 6982,09 | 12079,85 | 16467,08 | 20651,09 | 24744,15 | 28787,92 | 32801,79 | Km | |
| 5 | 3 | 3054,02 | 8151,78 | 12539,00 | 16723,02 | 20816,08 | 24859,84 | 28873,72 | Km | |
| 5 | 4 | 1769,14 | 6034,47 | 10119,80 | 14139,89 | 18128,57 | 22099,64 | 26059,83 | Km | |
| 5 | 5 | 1500,39 | 5428,47 | 9356,54 | 13284,62 | 17212,69 | 21140,76 | 25068,84 | Km | |
| Das Buch enthält eine Tabelle der Schichtungen für n < 11 |
| In der obigen Tabelle sind für n=2 und k=3 sowie für n=3 und k=2 und k=3 keine Einträge vorhanden, da hier lediglich schon vorhandene Frequenzen erzeugt werden. Bemerkenswert ist, das in der Distanztabelle der Grundhüllenradius R=Lo für alle n bei k=1 auftritt. Diese Tabelle wird für die weiteren Betrachtungen und Auswertungen noch genutzt. |
| Die berechneten Distanzen aus der Tabelle in Kapitel
12.2 kann man umsortieren und zwar ihrer
Größe entsprechend. Dadurch entsteht
die Möglichkeit einer Auswertung: Innerhalb frei wählbarer Distanzabschnitte (vom Erdmittelpunkt aus gesehen) fällt nur eine begrenzte Anzahl von Schichten an, wenn die Parameter n und k in der Gleichung endlich sind. Aus der gegebenen Distanz und der Anzahl der vorhandenen Schichten lässt sich der allgemeine Durchschnitt der Schichtendistanzen bestimmen. Die jeweilige reale Verteilung der Schichten führt in bestimmten Bereichen zu Verdichtungen. D.h. auf einer relativ kurzen Distanz kommen mehr Schichten vor als im allgemeinen Durchschnitt. Aus diesen Verdichtungen lassen sich Mittelwerte bilden, die dann quasi das Spektrum der maximal möglichen Schichtenbildung ergeben. |
| Es wird dabei weder die Polarität noch die Interferenz der Schichten berücksichtigt, sondern lediglich deren Häufigkeit. Das Spektrum der maximal möglichen Schichtenbildung lässt sich aber auch so, ohne Einschränkung der Allgemeinheit, für einen Vergleich mit der Erde nutzen. Folglich kann der Schalenaufbau der Erde und die Schichtungen der Atmosphäre direkt mit dem Spektrum vergleichen werden. Dies geschieht in den nächsten Kapiteln 13 und 14. |
| Im Buch wird noch eine zweite Gleichung für die magnetischen Schichten angegeben. |
| In den Kapitel 5 und Kapitel 6 konnte, durch das
Grundfeldmodell, gezeigt werden dass sich mit den
Grundfrequenzen der Erde auch gewisse magnetische
Strukturen etabliert haben, die als tesserale
Kugelflächenfunktionen beschreibbar sind. Oder auch als
Globalnetzgitter (GNG) bekannt sind. Aus den Kapiteln 11 und 12 folgt, dass sich mit den Grundfrequenzen der Erde und den Globalnetzgittern bestimmte dreidimensionale (elektro) magnetische Schwingungsstrukturen gebildet haben, die man als räumliche radiale Schwingungssysteme mit einer Gitterstruktur bezeichnen kann. Oder die man auch näherungsweise als Kubensysteme benennen kann. Mit der Fourieranalyse des Erdmagnetfeldes, aus den Kapitel 8, Kapitel 9 und Kapitel 10 bestätigt sich einerseits die Gitterstruktur des Erdmagnetfeldes und zeigt andererseits das magnetische Intensitäten, in Abhängigkeit von der Frequenz, in der gesamten Schwingungsstruktur eine erhebliche Rolle spielen. Bisher erfolgt bei magnetischen Messungen stets die Bestimmung der magnetischen Gesamtflussdichte, d.h. eine Quantifizierung der lokalen magnetischen Flussdichte über alle Frequenzen hinweg. Dies liegt einerseits am physikalischen Ansatz, der von einer zeitlich quasi konstanten Flussdichte ausgeht und dadurch bedingt andererseits am Aufbau der benutzten Mess-Sonde. Somit wird aber stets nur die Summe aller Anteile gemessen. |
| Wie aber die Fourieranalyse zeigt, existieren ein zonaler, ein sektorieller und ein tesseraler Schwingungsanteil, die in ihrer Intensität auch noch unterschiedlich sind. Wobei Hartmann durch seinen Versuch mit einer Hall-Sonde (Kapitel 11.1) den Zusammenhang zwischen den Gittern und dem zonalen Anteil ja schon nachgewiesen hat. |
| Und dazu liefert das gesamte Schwingungsmodell
folgenden Ansatz: Baut man Antennen und Empfänger, die (elektro)magnetische Intensität in Abhängigkeit von der Frequenz messen, so müssten sich damit die Globalnetzgitter der Erde und das räumliche radiale Schwingungssystem mit Gitterstruktur naturwissenschaftlich und technisch einwandfrei bestimmen lassen. Aus der Fourieranalyse ist ersichtlich das die auftretenden magnetischen Flussdichten sehr klein sind, zum größten Teil sogar kleiner als 1 μT. Die Messung der Globalnetzgitter über magnetische Intensitäten und Frequenzen liefert somit ein verifizierbares bzw. falsifizierbares Argument um das Modell des räumlich radialen Schwingungssystems mit Gitterstruktur belegen oder widerlegen zu können. |
| Bemerkenswert ist noch, das Nullflächen die Wände
des gitterförmigen Schwingungssystems bilden und die
Extrema sich punktförmig im Mittelpunkt des jeweils
einhüllenden Quaders befinden. Die Betrachtung als Kubensystem bedeutet immer eine Betrachtung der Nullwände. Man kann das System aber auch aus der Position der punktförmigen Extrema sehen. Dann bildet sich ein räumlich radiales Netz von Extremalpunkten, die die Erde durchsetzen und umhüllen. In der Struktur vergleichbar mit einem atomaren Gitter. Jedes Schwingungsatom besitzt dann eine ihm charakteristische Frequenz und Intensität. Diese Struktur nachzuweisen dürfte einfacher sein, als die Existenz der Nullwände zu zeigen. |
| Wie schon in Kapitel 5 erwähnt sind durch den
Sonnensatelliten Soho Bilder auf Radarbasis entstanden,
die eindeutig Grundfelder bzw. tesserale
Kugelflächenfunktionen auf der Sonnenoberfläche zeigen. Da erhebt sich die Frage ob das Magnetfeld der Erde nicht auch über Satelliten beobachtet werden könnte, die Fotografien in bestimmten Frequenzbereichen (Radar) machen. Es müssten nämlich bestimmte Frequenzbereiche existieren, mit denen es möglich ist quasi Fotos der magnetischen Gittersysteme zu erhalten. Dies ließe sich für ein Ortungssystem nutzen, um z.B. unterirdische Objekte (Anlagen, Bunker, Bodenschätze) oder untergetauchte U-Boote ausfindig zu machen. Jedes größere Objekt hat kapazitive (Kunststoffe) und/oder induktive (Metalle) Eigenschaften. Dies führt zu einer lokalen Verzerrung der Gitter und wenn diese Verzerrung detektiert werden kann, dann ist auch die gesamte Stealth-Technologie so gut wie nutzlos. Von Vögeln weiß man das die magnetische Orientierung mit ihrem Sehen, also den Augen, gekoppelt ist. Es existieren eine Reihe von Publikationen zu diesem Thema. Beispielhaft seien hier nur die Untersuchungen von Wiltschko genannt. (siehe Wiltschko, Möller, Gesson, Noll, Wiltschko, 2004 / Wiltschko, Gesson, Stapput, Wiltschko, 2004 / Wiltschko, Ritz, Stapput, Thalau, Wiltschko, 2005) Siehe dazu auch Kapitel 18.17 Es gibt eine Publikation von D. T. Edmonds aus dem Jahr 1992 mit dem Titel „A magnetic null detector as the migrating bird’s compass“ erschienen im „Proc. R. Soc. Lond. B 249“ Seiten 27–31, in der ein Nullwertdetektor für das magnetische Feld bei Zugvögeln beschrieben wird. Daher besteht eine gewisse Wahrscheinlichkeit das Zugvögel die Gitter, speziell die Nullzonen, wahrnehmen können. Die Frage ist, ob sich das auch in einen technischen Sensor umwandeln lässt. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |