Copyright © Klaus Piontzik
| Die Grundbedingung nach Kapitel 5.2 ist, das eine ganze Anzahl von Schwingungen einmal um die Erde passt und so eine stehende Welle, als stationärer Zustand, auftritt. In einem ersten Ansatz gilt für die Oberfläche: |
Wellenlänge = Umfang/Anzahl der Schwingungen |
| Die Wellenläge entspricht einer bestimmten Strecke auf dem Umfang der Erde. In der folgenden Abbildung 6.1 ist die Situation für eine Schwingung veranschaulicht. Die beiden Punkte A und C sind die Endpunkte des Kreisbogens s, der gleichzeitig auch eine Wellenlänge λ darstellt. |
 |
und |  |
| Betrachtet man diese Situation vom Erdmittelpunkt aus, so lässt sich jeder Schwingung ein bestimmter Winkel α zuordnen. |
 |
| Insgesamt als Grundlage gilt dann: |
 |
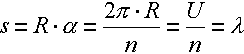| Aus Gründen der Veranschaulichung ist, bei der bisherigen Darstellung, ein Faktor unbeachtet geblieben, der nun in die Betrachtung einbezogen werden muss: die Kugelgestalt der Erde. Es muss noch berücksichtigt werden das die Wellenausbreitung linear stattfindet, und nicht entlang der gekrümmten Erdoberfläche. In der Konsequenz ergibt sich daher eine Modifikation der Grundgleichung. |
 |
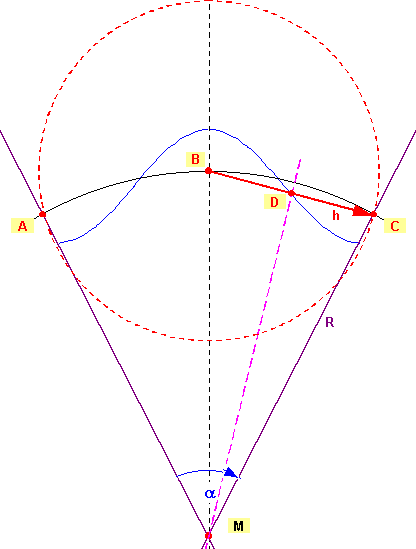| Abbildung 6.1 - Wellenlänge und Umfang |
| Nach dem Huygenschen Prinzip dienen die Punkte A, B,
C in Abb.6.1, also die Extremalpunkte, als Quellpunkte
der stehenden Welle. Elektromagnetische Wellen breiten sich kugelförmig von einem Punkt aus. Wenn Punkt B der Ausgangspunkt ist, so entspricht die Strecke BDC = h dem Weg der Welle. Da ein stationärer Zustand herrscht, genügt es den Weg der Welle von einer Quelle zur nächsten Quelle zu betrachten. |
 |
| Das Dreieck MCD ist rechtwinklig im Punkt D und es gilt: |
 |
 |
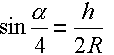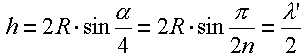| Umstellen nach lambda strich ergibt die korrigierte Wellenlänge: |
 |
| Der Zusammenhang zwischen Frequenz und Wellenlänge lautet: |
| f · λ = c |
| Damit ergibt sich die Gleichung für die Erdfrequenzen: |
 |
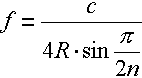| c
steht für die Lichtgeschwindigkeit, R für den Radius der Erde,
n fürdie Anzahl der
Schwingungen Da die Erde aber keine vollkommene Kugel ist, da an den Polen abgeplattet, existieren hier zwei Radien: der Polradius und der Äquatorradius. Und daraus resultieren auch zwei (leicht voneinander abweichende) Grundfrequenzen. Das Geodätischen Referenzsystems WGS84 beruht auf einem Sphäroid, also einem Rotationsellipsoid. Siehe dazu Kapitel 17.1 Die Daten des Geodätischen Referenzsystems WGS84 lauten: Polradius: 6356752 m Äquatorradius: 6378137 m Abplattung: 1:298,2572 Mit c = 299792458 m/s als Lichtgeschwindigkeit ergibt sich mit n = 1 für die einzelnen Radien: |
|
Polradius : 11,79 Hertz Äquatorradius : 11,75 Hertz |
| Die auftretende Differenz mag auf den ersten Blick
unerheblich erscheinen. Bei weiterer Betrachtung ergibt
sich aber ein bedeutsamer Unterschied. Im nächsten
Kapitel 7 wird dies am Thema Sferics noch deutlich
erkennbar werden. Bemerkung: Nikolas Tesla gab seinerzeit die Erdfrequenz „bei etwa 12 Hz liegend“ an. |
| Ein weiterer Zusammenhang zur Polachse ist durch die Grundschwingung gegeben. Gibt man für die ersten Grundfrequenzen die allgemeinen Lösungen an, so lauten diese: |
| n | f | Polradius | Äquatorradius |
| 1 |  |
11,79 Hz | 11,75 Hz |
| 2 |  |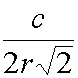
16,674 Hz | 16,618 Hz |
| 3 |  |
23,58 Hz | 23,5 Hz |
| Für n=1
lautet die allgemeine Gleichung für die Wellenlänge: λ = 4R Und das gleiche Ergebnis erhält man, wenn eine Strecke von der Länge des Poldurchmessers an beiden Enden frei schwingen würde. So wie in der folgenden Abbildung 6.2 dargestellt. |
 |
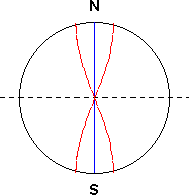| Abbildung 6.2 - Erde und Grundschwingung |
| Das Analogon hier ist ein massiver Stab, dessen beiden Enden frei sind. Wird dieser Stab nun in Schwingung versetzt, so entspricht die Grundschwingung der einsetzenden longitudinalen Biegeschwingungen dem Bild 6.2. (siehe dazu auch „Physik“ von Gerthsen, Kneser, Vogel – Kapitel 4.1.5) |
| Setzt man nacheinander für n die Werte 1,2,3... in obige Gleichung für die Frequenz ein, so ergeben sich die Grundfrequenzen der Erde. Die folgende Tabelle enthält die ersten 30 Frequenzen bezogen auf den Polradius. |
| n | Polradius |
| 1 | 11,7903 Hz |
| 2 | 16,6740 Hz |
| 3 | 23,5806 Hz |
| 4 | 30,8095 Hz |
| 5 | 38,1542 Hz |
| 6 | 45,5542 Hz |
| 7 | 52,9850 Hz |
| 8 | 60,4350 Hz |
| 9 | 67,8975 Hz |
| 10 | 75,3688 Hz |
| 11 | 82,8465 Hz |
| 12 | 90,3289 Hz |
| 13 | 97,8149 Hz |
| 14 | 105,3038 Hz |
| 15 | 112,7949 Hz |
| 16 | 120,2880 Hz |
| 17 | 127,7825 Hz |
| 18 | 135,2783 Hz |
| 19 | 142,7752 Hz |
| 20 | 150,2730 Hz |
| 21 | 157,7715 Hz |
| 22 | 165,2708 Hz |
| 23 | 172,7706 Hz |
| 24 | 180,2709 Hz |
| 25 | 187,7717 Hz |
| 26 | 195,2729 Hz |
| 27 | 202,7744 Hz |
| 28 | 210,2762 Hz |
| 29 | 217,7784 Hz |
| 30 | 225,2807 Hz |
| Zu diesen Grundfrequenzen treten noch
entsprechende Oberwellen auf, d.h. man muss dazu nur die
ganzzahligen Vielfachen bilden. (Als Oberwellen bezeichnet man allgemein ganzzahlige Vielfache einer gewählten Grundfrequenz) |
| Im Buch werden noch die Frequenzen bezogen auf den Äquatorradius angegeben. |
| Im Buch wird noch die Ableitung für eine weitere Frequenzgleichung angegeben. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
