Copyright © Klaus Piontzik
|
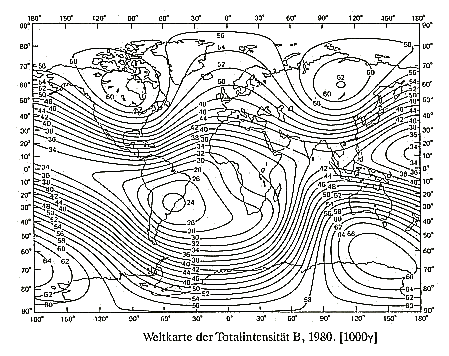
Ausgangspunkt der Fourieranalyse ist das Feld der
Totalintensität, wie es im Kapitel 2– Abb.2.1
schon vorgestellt wurde und in Bild 8.1
noch einmal dargestellt wird (IGRF 1980). Mittels dieser
Grafik wurde eine Tabelle für die Werte der
Totalintensität generiert.
Voraussetzung: |
|
Längengrad: -180° ≤ λ' ≤ +180° Breitengrad: -90° ≤ φ' ≤ +90° |
 |
Eine Tabelle für die ermittelten Werte
lässt sich hier finden:
TABELLE DES
ERDFELDES
Das Gesamtfeld wird in einzelne waagerechte Schnitte zerlegt. Jeder Schnitt verläuft entlang eines Breitenkreises. Nullpunkt ist dabei der im Kapitel 4 ermittelte Anfangswert von -13,5 Grad West. Von +90 Grad Nord bis -90 Grad Süd wurden die Schnitte im Abstand von 7,5 Grad angelegt. Dies ergibt dann 24 Schnitte |
|
| Abbildung 8.1 - Weltkarte der magnetischen Totalintensität |
|
Jeden Schnitt unterzieht man einer
eindimensionalen (numerischen) Fourieranalyse, mit der
Variablen λ (Lambda) und der Schrittweite 7,5 Grad, d.h. mit
48 Punkten pro Schnitt. Es ergeben sich so insgesamt 1106
Punkte für die Analyse des Erdfeldes.
Als Grundlage bzw. Werkzeug der gesamten Analyse dient ein numerisches (eindimensionales) harmonisches Verfahren, wie es im Buch „Mathematik für Ingenieure“ von Brauch/Dreyer/Haacke beschrieben wird und auch als Algorithmus von Goertzel (und Reinsch) bekannt ist. Das eindimensionale numerische Verfahren funktioniert mit einem Winkel von 0 bis 360 Grad. Für diese erste numerische harmonische Analyse der Schnitte entlang der Breitenkreise, also mit dem Längengrad λ strich, ist die Bedingung für den Wertebereich erfüllt. Lediglich der Parameter λ strich muss angepasst werden. Es gilt: |
 |
| Dieses Verfahren liefert zu einer gegebenen Zahlenfolge, also hier den Werten eines Schnittes, die entsprechenden Fourierkoeffizienten. Mit diesen Koeffizienten lassen sich die Schnitte als Summe von Winkelfunktionen darstellen. |
| Dann lassen sich die 24 Schnitte, durch die erste Fourieranalyse bedingt, allgemein so darstellen: |
 |
bis |  |
| Schreibt man diese Gleichungen aus, so ergibt sich folgendes Bild: |
 |
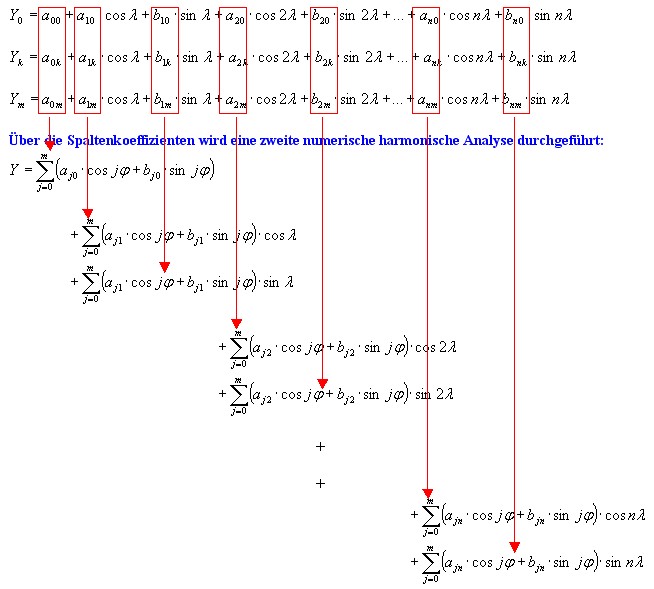| Durch die erste numerische harmonische Analyse ensteht allgemein ein Gleichungssystem von m+1 Gleichingen mit jeweils n+1 Gliedern. Dann lässt sich über die Spalten der Koeffizientenmatrix (mit den Am und Bm) eine weitere Fourieranalyse, mit der Variablen φ (Phi), durchführen. Diese zweite numerische harmonische Analyse liefert die Endkoeffizienten mit den Aji und Bji | |
 |
|
| Wenn man den zonal, sektoriellen Teil vom tesseralen Anteil trennt, ergibt sich für jeden Punkt auf der Erde mit den Parametern λ, φ (Lambda, Phi) dann: | |
 |
| Achtung: Im Buch ist in dieser Gleichung ein Druckfehler aufgetreten !!! | |
| Der erste Term für Y (also der zonal, sektorielle Teil) lässt sich noch so ergänzen: | |
 |
 |
| Dann lässt sich die qualitative Endgleichung für einen Punkt auf der Erdoberfläche so darstellen: |
 |
| Zu beachten ist hier, dass λ, φ (Lambda, Phi) nicht direkt
die geographischen Koordinaten darstellen, sondern
Parameter sind, die diese Koordinaten repräsentieren. Multipliziert man die Klammern aus, so treten lediglich Terme auf die Sinus- und Cosinusfunktionen enthalten, die multiplikativ miteinander verknüpft sind. Also Kugelflächenfunftionen bzw. Gitter. |
| Das Magnetfeld der Erde lässt sich durch eine Summe von Gittern beschreiben |
| Eine quantitative Auswertung der angegebenen Tabelle des Erdmagnetfeldes mittels der beschriebenen numerischen Fourieranalyse erzeugt, für die erdmagnetische Flussdichte B, folgendes Ergebnis: |
| alle Werte in μT (mükrotesla) |
|
| Wie an den Variablen zu sehen ist zerlegt sich das
Magnetfeld in einen statischen,
einen sektoriellen
(BS), einen zonalen (BZ)
und einen tesseralen
(BT) Anteil
(siehe Kapitel 5).
Es treten lediglich Terme auf die auch in der Gleichung von Gauß enthalten sind (siehe Kapitel 2.7). Es gilt dann: |
| B = 47,2183 + BZ + BS + BT μT (mükrotesla) |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
