Copyright © Klaus Piontzik
 |
Das Gesamtfeld lässt sich, wie bisher
gesehen, durch die Dipoltheorie allein nicht erklären.
Die herkömmliche Forschung umgeht das Problem
mathematisch, indem sie das Dipolfeld vom Gesamtfeld
abzieht und das sogenannte Differenzfeld betrachtet, wie
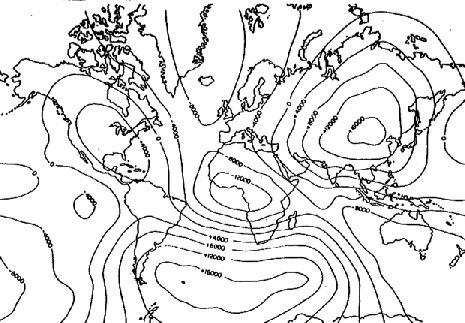
in Abb.3.1 dargestellt. Dieses Feld wird oft als Nicht-Dipolfeld (bzw. Non-Dipol) bezeichnet und macht etwa 14-16% der Intensität des Gesamtfeldes aus. |
|
| Abbildung 3.1 - Das Differenzfeld | ||
| Die Handhabung des Differenzfeldes ist insofern
problematisch, da die Dipoltheorie ja ein Teil der
Betrachtung ist. Wie beim Gesamtfeld besteht die Möglichkeit, die Intensitäten der Abbildung 3.1 in eine numerische Tabelle zu übertragen. Aus der Gesamtwerttabelle und der Dipolgleichung kann diese Tabelle aber auch berechnet werden. Interessant am Differenzfeld sind die Koordinaten der neuen Extremwerte mit Stand 1980. |
| Name | Breite |
Länge |
| Nord-Maximum | +45,2485 Grad Nord | -95,7685 Grad West |
| Süd-Maximum | -41,371 Grad Süd | +129,21 Grad Ost |
| Grosse Anomalie | +45,126 Grad Nord | +99,7395 Grad Ost |
| Minimum | -52,318 Grad Süd | +8,6395 Grad West |
| Nordmaximum und Anomalie haben eine
geographische Breite von 45 Grad. Würden sie sich noch
genau gegenüber liegen, so bildeten sie die Eckpunkte
eines Tetraeders, der in die Erde eingeschrieben ist.
Anomalie und Nordmaximum sind aber in der Länge um etwa
15 Grad gegeneinander verschoben. Vergleicht man die weiteren Tetraederpunkte, so ergibt sich in etwa eine Übereinstimmung des Minimums für die geographische Länge. Die geographische Breite weicht jedoch um etwa 7 Grad von der Tetraederposition ab. Das Minimum liegt also lediglich in der Nähe des dritten Tetraederpunktes. Das Südmaximum stimmt zwar in der Breite in etwa mit der Tetraederstruktur überein. Die geographische Länge weicht hier jedoch um etwa 20 Grad von der Tetraederposition ab. Auch das Südmaximum liegt also lediglich in der Nähe des vierten Tetraederpunktes. Dies liefert auch einen ersten Hinweis darauf, dass eine Tetraederstruktur zwar vorhanden ist, allein aber noch nicht ausreicht, um das gesamte Feld zu erklären. Insgesamt kann man daraus die Schlussfolgerung ziehen, das auch hier weitere Einflüsse vorhanden sein müssen, die die reine Tetraederstruktur stören und verzerren. |
| Wie im Buch in Kapitel 1.2 zu sehen
ist wandert die Dipolachse sehr stark und das verändert
auch das Differenzfeld, so dass heute eine etwas andere
Struktur gegeben ist. Für eine langfristige Analyse ist das Differenzfeld daher denkbar ungeeignet. Wie am Gesamtfeld (Kapitel 2.3) im Buch gezeigt wird, ist dieses über lange Zeiträume quasi konstant und daher viel besser für eine allgemeine Analyse nutzbar. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
