Bestimmung der geographischen Länge von Gizeh

Mit Hilfe der Satellitengeodäsie sind, 1966 durch C.A. Lundquist und G. Veis, folgende Parameter ermittelt worden:

a₁ ist dabei die große Äquatorhalbachse, a₂ die kleine Äquatorhalbachse und Lo die geographische Länge der großen Halbachse.Siehe dazu auch: Gestalt der Erde-4 - Dreiachsige Ellipsoide

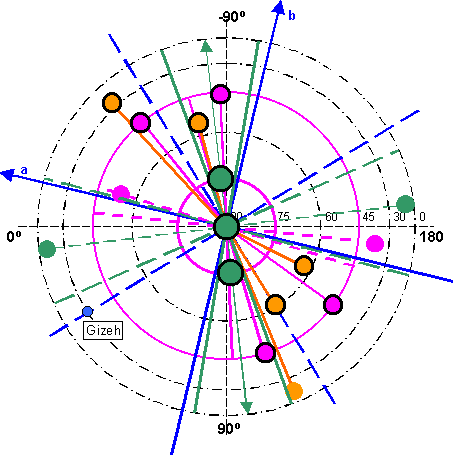
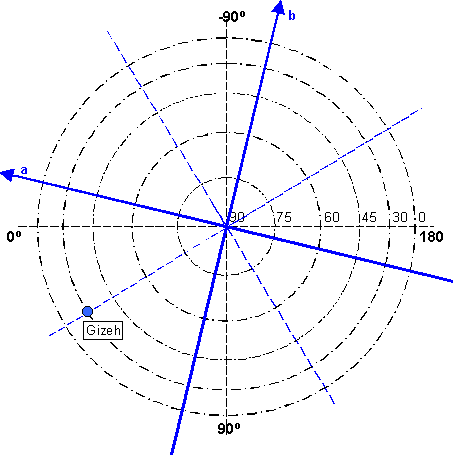
		Trägt man nun die Position von Gizeh in ein Koordinatensystem ein, das an das dreiachsige Ellipsoid anlehnt, ergibt sich das nebenstehende Bild. Gizeh liegt dann etwa auf der 45 Grad Position in Länge. Das Gleiche lässt sich von Heliopolis sagen
Abbildung 2.1 - Achsen des dreiachsigen Ellipsoids und Gizeh

2.2 - Das Magnetfeld

Betrachtet man die Erde von oben aus, und zwar so dass man auf den Nord- bzw. Südpol hinunter schaut und trägt bestimmte Breitenkreise (0,30,45,60 Grad) auf, so erhält man ein radiales Koordinatensystem.

Einzeichnen der Achsen für ein dreiachsige Ellipsoid (das blaue kartesische Koordinatensystem) und Eintragen aller magnetischen Extremwerte ergibt das folgende Bild:. Siehe dazu auch: Gestalt der Erde und Magnetfeld

		Nimmt man nun den Wert von Lundquist und Veis, und vergleicht diesen mit dem Nullpunkt (-13,5 Grad als geographische Längenposition) des magnetischen Systems lässt sich, global gesehen, eine gute Übereinstimmung feststellen. Auch hier nimmt Gizeh eine exponierte Stellung zwischen den magnetischen Extrema ein und liegt bei etwa 45 Grad Länge
Abbildung 2.2 - Achsen des Magnetfeldes und Gizeh

Nimmt man umgekehrt Gizeh als genaue 45 Grad-Marke dann ergibt sich die Position der grossen Halbachse zu: Lo = -13° 51` Nimmt man Heliopolis als genaue 45 Grad-Marke dann ergibt sich die Position der grossen Halbachse zu: Lo = -13° 41`

Tabelle der möglichen Nullpunkte in Länge

geodätisch	Lo = -14° 45`
Gizeh	Lo = -13° 51`
Heliopolis	Lo = -13° 41`
magnetisch	Lo = -13° 30`

Gizeh liegt, orientiert an einem dreiachsigen Ellipsoid, auf etwa 45 Grad östlicher Länge

2.3 - Die Mittelwertpunkte der Erde

Eine geodätische Betrachtung der Mittelwertpunkte lässt sich unter "Die Gestalt der Erde-13 - Mittelwerte und Erdgestalt" nachschlagen. Eine Ableitung der Mittelwertpunkte lässt sich unter "Die Gestalt der Erde-12 - Mittelwerte der Ellipse" nachsehen.

Wertet man alle Mittelwerte aus, die an einer Ellipse, bezüglich der Achsen, möglich sind, so ergeben sich fünf Fälle.
Diese sind in der folgenden Tabelle aufgeführt. Die Werte sind dabei gerundet, da alle Mittelwerte lediglich ein paar Bogensekunden bzw. Bogenminuten von den angegebenen Zahlenwerten abweichen.
Die Art der Mittelwertbildung ist dabei beliebig. Daher wird hier nicht mehr zwischen den einzelnen Mittelwerten unterschieden, sondern die Mittelwerte allgemein mit M bezeichnet.

FALL	Mittelwertbedingung	Winkel

I	R=M	45°
II	y=M/2	30°
III	x=M/2	60°
IV	x=M	3°
V	y=M	-

Tabelle 2.1

Bemerkenswert ist, dass für y = M keine Mittelwerte existieren, da alle Mittelwerte grösser als die kleine Halbachse sind und daher ausserhalb der Ellipse liegen.
Zeichnet man alle vorhandenen Mittelwerte in die Ellipse ein, so ergibt sich folgende Abbildung:

Abbildung 2.3 - Ellipse und ihre Mittelwerte

Nimmt man als Erdmodell ein Rotationsellipsoid, so ergeben die Mittelwerte aus der Abbildung ausgezeichnete Breitengrade.

Nimmt man ein dreiachsiges Ellipsoid als Erdmodell (Werte von Lundquist und Veist), so ergeben sich einzelne Punkte. Diese Punkte werden ab als Mittelwertpunkte bezeichnet.
Trägt man alle Mittelwertpunkte in eine Zeichnung der Erde ein, so ergibt sich die nächste Abbildung

Gizeh bzw. Heliopolis gehören zu den Mittelwertpunkten der Erde

Abbildung 2.4 - Erde und Mittelwertpunkte

2 - Bestimmung der geographischen Länge von Gizeh

2.1 - Die Gestalt der Erde als dreiachsiges Ellipsoid

2.2 - Das Magnetfeld

2.3 - Die Mittelwertpunkte der Erde